题目内容
6.已知一次函数f(x)=kx+2与反比例函数g(x)=$\frac{m}{x}$的图象交于两点P(3,-1)、Q(x0,y0)(1)求k,m值及Q点坐标
(2)当x>0时,试写出f(x)>g(x)的解集.
分析 (1)把点P的坐标代入f(x)、g(x)的解析式,求得m、k的值,再解方程组求得Q的坐标.
(2)由题意可得f(x)的图象在g(x)的图象的上方,结合图象求得x的范围.
解答 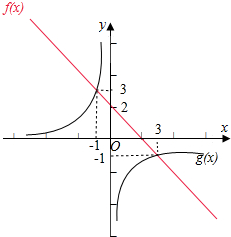 解:(1)根据f(x)=kx+2与反比例函数g(x)=$\frac{m}{x}$的图象交于两点P(3,-1)、Q(x0,y0),
解:(1)根据f(x)=kx+2与反比例函数g(x)=$\frac{m}{x}$的图象交于两点P(3,-1)、Q(x0,y0),
可得$\frac{m}{3}$=-1,即 m=-3,g(x)=$\frac{-3}{x}$;再由 3k+2=-1,求得k=-1,可得 f(x)=-x+2.
再由$\left\{\begin{array}{l}{y=-x+2}\\{y=\frac{-3}{x}}\end{array}\right.$,求得 $\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$,或 $\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$.
结合条件可得,Q点坐标为(-1,3).
(2)当x>0时,由f(x)>g(x)可得,f(x)的图象在g(x)的图象的上方,
结合图象可得0<x<3,即 f(x)>g(x)的解集为{x|0<x<3}.
点评 本题主要考查其它不等式的解法,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
14.设f(x)=3x2-x+1,g(x)=2x2+x-1,x∈R,则f(x)与g(x)的大小关系是( )
| A. | f(x)>g(x) | B. | f(x)≥g(x) | C. | f(x)=g(x) | D. | f(x)<g(x) |
18.不等式组$\left\{\begin{array}{l}{|x-1|-3<0}\\{a-2x>0}\end{array}\right.$的解集为{x|-2<x<4},则a的取值范围是( )
| A. | a≤-4 | B. | a≥-4 | C. | a≤8 | D. | a≥8 |
15.已知双曲线Γ:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点为A,与x轴平行的直线交Γ于B,C两点,记∠BAC=θ,若Γ的离心率为$\sqrt{2}$,则( )
| A. | θ∈(0,$\frac{π}{2}$) | B. | θ=$\frac{π}{2}$ | C. | θ∈($\frac{3π}{4}$,π) | D. | θ=$\frac{3π}{4}$ |