题目内容
16.若O在△ABC的内部,且满足$\overrightarrow{AO}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AC}$,求△AOC与△ABC的面积之比为1:3.分析 可取AC中点D,然后连接OD,并作OE∥AC,从而根据向量加法的平行四边形法则以及已知条件即可得出OD:AB=1:3,这样即可得出△AOC与△ABC的面积之比.
解答 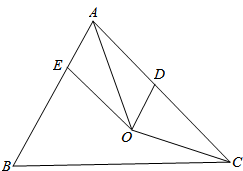 解:如图,
解:如图,
取AC中点D,连接OD,过O作OE∥AC,交AB于E;
∴根据$\overrightarrow{AO}=\frac{1}{3}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$得$AE=\frac{1}{3}AB$,AE=OD;
∴$OD=\frac{1}{3}AB$;
∴S△AOC:S△ABC=1:3.
故答案为:1:3.
点评 考查向量数乘的几何意义,向量加法的平行四边形法则,以及三角形的面积公式.

练习册系列答案
相关题目
8.盒子里共有大小相同的3只白球,1只黑球.若从中随机摸出两只球,则它们颜色不同的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
5.已知在△ABC中,3sinA+4cosB=6,4sinB+3cosA=1,则sinC=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{{\sqrt{3}}}{2}$ | D. | -$\frac{{\sqrt{3}}}{3}$ |