题目内容
【题目】已知函数f(x)的图像与函数h(x)=
的图像关于点Ａ（0，1）对称。
（１）求函数f(x)的解析式；
（２）若g(x)＝xf(x)＋ax，且g(x)在区间（0,4］上为减函数，求实数a的取值范围。
【答案】（1）
；（2）(－∞，－10].
【解析】试题分析：（1）利用函数关于点A（0，1）对称，求出函数的解析式．
（2）利用二次函数的图象和性质得到对称轴与区间的关系．
试题解析：
(1)∵f(x)的图象与h(x)的图象关于点A(0,1)对称，设f(x)图象上任意一点坐标为B(x，y)，其关于A(0,1)的对称点B′(x′，y′)，
则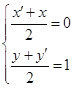
∴ 
∵B′(x′，y′)在h(x)上，∴y′＝x′＋
.
∴2－y＝－x－
，∴y＝x＋ +2，
即f(x) ＝x＋ +2.
(2)∵g(x)＝xf(x)+ax=x2+(a+2)x+1且g(x)在(0,4]上为减函数，
∴
≥4，
即a≤－10.
∴a的取值范围为(－∞，－10]．
练习册系列答案
名校课堂系列答案
相关题目
