题目内容
【题目】在直角坐标系xOy中,l是过定点P(4,2)且倾斜角为α的直线;在极坐标系(以坐标原点O为极点,
以x轴非负半轴为极轴,取相同单位长度)中,曲线C的极坐标方程为![]() .
.
(1)写出直线l的参数方程,并将曲线C的方程化为直角坐标方程;
(2)若曲线C与直线相交于不同的两点M,N,求|PM|+|PN|的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据![]() 直接写出
直接写出![]() 的参数方程,利用极坐标与直角坐标的转换关系式
的参数方程,利用极坐标与直角坐标的转换关系式![]() ,可将曲线C的方程化为直角坐标方程;(2)联立
,可将曲线C的方程化为直角坐标方程;(2)联立![]() 的参数方程与曲线
的参数方程与曲线![]() 的普通方程,消去
的普通方程,消去![]() 与
与![]() ,得到关于
,得到关于![]() 的一元二次方程,写出
的一元二次方程,写出![]() 关于
关于![]() 及
及![]() 的表达式,利用韦达定理及
的表达式,利用韦达定理及![]() 的范围,可探求
的范围,可探求![]() 的取值范围.
的取值范围.
试题解析:(1)直线l的参数方程为![]() (t为参数).
(t为参数).
∵ρ=4cos θ,∴ρ2=4ρcos θ,所以C:x2+y2=4x.
(2)直线l的参数方程为![]() (t为参数),代入C:x2+y2=4x,得
(t为参数),代入C:x2+y2=4x,得
t2+4(sin α+cos α)t+4=0,
则有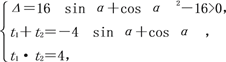 ∴sin α·cos α>0,又α∈[0,π),
∴sin α·cos α>0,又α∈[0,π),
所以α∈![]() ,t1<0,t2<0.
,t1<0,t2<0.
而|PM|+|PN|=![]() +
+
![]() =|t1|+|t2|
=|t1|+|t2|
=-t1-t2=4(sin α+cos α)=4![]() sin
sin![]() .
.
∵α∈![]() ,∴α+
,∴α+![]() ∈
∈![]() ,∴
,∴![]() <sin
<sin![]() ≤1,
≤1,
所以|PM|+|PN|的取值范围为(4,4![]() ].
].

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目