题目内容
（2013•重庆）设f（x）=a（x﹣5）2+6lnx，其中a∈R，曲线y=f（x）在点（1，f（1））处的切线与y轴相交于点（0，6）．
（1）确定a的值；
（2）求函数f（x）的单调区间与极值．
（1）确定a的值；
（2）求函数f（x）的单调区间与极值．
（1）
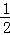（2）见解析
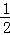（2）见解析（1）因f（x）=a（x﹣5）2+6lnx，故f′（x）=2a（x﹣5）+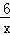
，（x＞0），
令x=1，得f（1）=16a，f′（1）=6﹣8a，
∴曲线y=f（x）在点（1，f（1））处的切线方程为y﹣16a=（6﹣8a）（x﹣1），
由切线与y轴相交于点（0，6）．
∴6﹣16a=8a﹣6，
∴a=．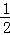
（2）由（1）得f（x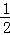）=（x﹣5）2+6lnx，（x＞0），
f′（x）=（x﹣5）+=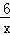
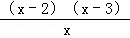，令f′（x）=0，得x=2或x=3，
当0＜x＜2或x＞3时，f′（x）＞0，故f（x）在（0，2），（3，+∞）上为增函数，
当2＜x＜3时，f′（x）＜0，故f（x）在（2，3）上为减函数，
故f（x）在x=2时取得极大值f（2）=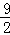
+6ln2，在x=3时取得极小值f（3）=2+6ln3．
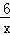，（x＞0），令x=1，得f（1）=16a，f′（1）=6﹣8a，
∴曲线y=f（x）在点（1，f（1））处的切线方程为y﹣16a=（6﹣8a）（x﹣1），
由切线与y轴相交于点（0，6）．
∴6﹣16a=8a﹣6，
∴a=
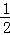．（2）由（1）得f（x）=
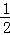（x﹣5）2+6lnx，（x＞0），f′（x）=（x﹣5）+
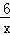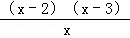=，令f′（x）=0，得x=2或x=3，当0＜x＜2或x＞3时，f′（x）＞0，故f（x）在（0，2），（3，+∞）上为增函数，
当2＜x＜3时，f′（x）＜0，故f（x）在（2，3）上为减函数，
故f（x）在x=2时取得极大值f（2）=
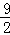+6ln2，在x=3时取得极小值f（3）=2+6ln3．
练习册系列答案
相关题目
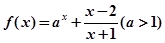
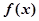在
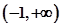上是增函数；
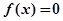没有负数根．
满足
（其中
为
处的导数，
为常数）．
，若函数
在
上单调，求实数
．
时，讨论
的单调性；
,当
若对任意
存在
使
求实数
的取值范围。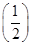
，c＝f(3)，则a，b，c的大小关系为____________．
为定义在(0，+∞)上的可导函数，且
恒成立，则不等式
的解集为______ _____．
，且
．
的值；
的单调区间；
，若函数
在
上单调递增，求实数
的取值范围．
R,求函数
在区间
上的最小值．
，3）内的图像如图所示．记y＝f（x）的导函数为y＝f¢（x），则不等式f¢（x）≤0的解集为（ ）
，1]∪[2，3）
]∪[
，
]