题目内容
已知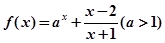
(1)证明函数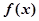 在
在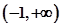 上是增函数;
上是增函数;
(2)用反证法证明方程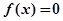 没有负数根.
没有负数根.
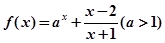
(1)证明函数
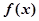 在
在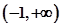 上是增函数;
上是增函数;(2)用反证法证明方程
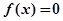 没有负数根.
没有负数根.(1)见解析 (2)见解析
试题分析:(1)利用导数求出函数的导函数
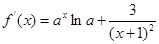 ,再由
,再由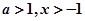 确定
确定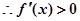 ;(2)假设存在负根,对原式进行变形得出
;(2)假设存在负根,对原式进行变形得出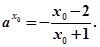 再由
再由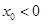 得出
得出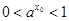 ,
,解出
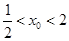 ,与假设矛盾得证.
,与假设矛盾得证.(1)
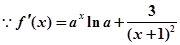 ,且已知
,且已知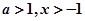 ,
, 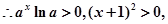
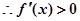 ,故函数
,故函数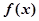 在
在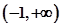 上是增函数.(注:也可以用单调性定义证明)
上是增函数.(注:也可以用单调性定义证明)(2)假设存在
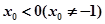 使
使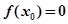 ,则
,则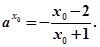
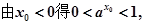 故
故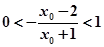 ,解得:
,解得: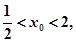 显然与
显然与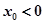 矛盾,
矛盾,所以使
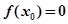 的
的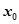 不存在,即方程
不存在,即方程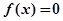 没有负数根.
没有负数根. 
练习册系列答案
相关题目
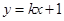 与曲线
与曲线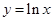 有公共点,则实数
有公共点,则实数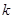 的取值范围是 .
的取值范围是 . 在区间(0,1)内任取两个实数p,q,且p≠q,不等式
在区间(0,1)内任取两个实数p,q,且p≠q,不等式 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )



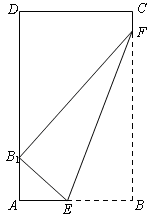
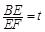 ,EF=l,l关于t的函数为
,EF=l,l关于t的函数为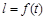 .
. 
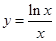 的最大值为( )
的最大值为( )



 在
在 上递增,则
上递增,则 的范围是( )
的范围是( )



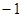 ,其中a≠0.若对一切x∈R,f(x)≥0恒成立,则a的取值集合 .
,其中a≠0.若对一切x∈R,f(x)≥0恒成立,则a的取值集合 .