题目内容
函数f(x)在定义域R内可导，若f(x)＝f(2－x)，且当x∈(－∞，1)时，(x－1)f′(x)<0，设a＝f(0)，b＝f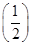
，c＝f(3)，则a，b，c的大小关系为____________．
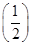，c＝f(3)，则a，b，c的大小关系为____________．c<a<b
依题意得，当x<1时，f′(x)>0，f(x)为增函数；又f(3)＝f(－1)，且－1<0<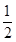
<1，因此有f(－1)<f(0)<f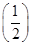，即有f(3)<f(0)<f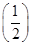，c<a<b.
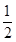<1，因此有f(－1)<f(0)<f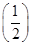，即有f(3)<f(0)<f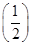，c<a<b.
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
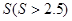平方米的矩形场地的围墙，要求在前面墙的正中间留一个宽度为2米的出入口，后面墙长度不超过20米，已知后面墙的造价为每米45元，其它墙的造价为每米180元，设后面墙长度为x米，修建此矩形场地围墙的总费用为
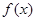元.
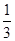x3＋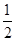
x2＋2ax，若f(x)在(
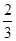，＋∞)上存在单调递增区间，则实数a的取值范围为( )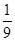
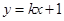与曲线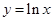
有公共点，则实数
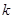的取值范围是 ．
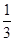x3－x2－3x＋
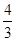，直线l：9x＋2y＋c＝0，若当x∈[－2,2]时，函数y＝f(x)的图象恒在直线l下方，则c的取值范围是________．
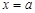和
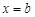是函数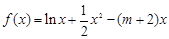
的两个极值点,其中
.
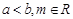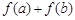的取值范围;
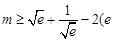为自然对数的底数),求
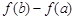的最大值.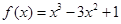
的单调递减区间为（ ）．
