题目内容
设椭圆C: (a>b>0)的离心率为
(a>b>0)的离心率为 ,过原点O斜率为1的直线与椭圆C相交于M,N两点,椭圆右焦点F到直线l的距离为
,过原点O斜率为1的直线与椭圆C相交于M,N两点,椭圆右焦点F到直线l的距离为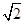 .
.
(1)求椭圆C的方程;
(2)设P是椭圆上异于M,N外的一点,当直线PM,PN的斜率存在且不为零时,记直线PM的斜率为k1,直线PN的斜率为k2,试探究k1·k2是否为定值?若是,求出定值;若不是,说明理由.
(1) ;(2) k1·k2是为定值-
;(2) k1·k2是为定值- .
.
解析试题分析:(1)由椭圆C: (a>b>0)的离心率为
(a>b>0)的离心率为 可得
可得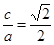 ,又由椭圆右焦点F(c,0)到直线l的距离为
,又由椭圆右焦点F(c,0)到直线l的距离为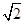 ,由点到直线的距离公式得
,由点到直线的距离公式得 =
=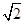 ,从而求得c的值,代入
,从而求得c的值,代入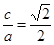 求得a的值;再注意到
求得a的值;再注意到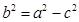 从而求得b的值,因此就可写出所求椭圆C的方程; (2)由过原点O斜率为1的直线方程为:y=x,联立椭圆C与直线L的方程就可求出M,N两点的坐标,再由过两点的直线的斜率公式就可用点P的坐标表示出kPM·kPN,再注意点P的坐标满足椭圆C的方程,从而就可求出k1·k2=kPM·kPN是否与点P的坐标有关,若与点P的坐标无关则k1·k2的值为定值;否则不为定值.
从而求得b的值,因此就可写出所求椭圆C的方程; (2)由过原点O斜率为1的直线方程为:y=x,联立椭圆C与直线L的方程就可求出M,N两点的坐标,再由过两点的直线的斜率公式就可用点P的坐标表示出kPM·kPN,再注意点P的坐标满足椭圆C的方程,从而就可求出k1·k2=kPM·kPN是否与点P的坐标有关,若与点P的坐标无关则k1·k2的值为定值;否则不为定值.
试题解析:(1)设椭圆的焦距为2c(c>0),焦点F(c,0),直线l:x-y=0,
F到l的距离为 =
=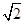 ,解得c=2,
,解得c=2,
又∵e=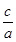 =
= ,∴a=2
,∴a=2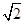 ,∴b=2.
,∴b=2.
∴椭圆C的方程为 .
.
(2)由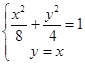 解得x=y=
解得x=y= ,或x=y=-
,或x=y=- ,
,
不妨设M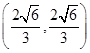 ,N
,N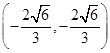 ,P(x,y),
,P(x,y),
∴kPM·kPN=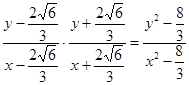
由 ,即
,即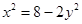 ,代入化简得k1·k2=kPM·kPN=-
,代入化简得k1·k2=kPM·kPN=- 为定值.
为定值.
考点:1.椭圆的标准方程;2.直线与椭圆的位置关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ﹣
﹣ |的值;
|的值;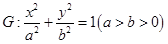 过
过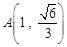 和点
和点 .
. 的方程;
的方程; 的直线
的直线 与椭圆
与椭圆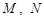 两点,且
两点,且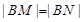 ,求直线
,求直线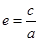 ,叫做椭圆的离心率.若两个椭圆的离心率
,叫做椭圆的离心率.若两个椭圆的离心率 相同,称这两个椭圆相似.
相同,称这两个椭圆相似. 与椭圆
与椭圆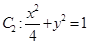 是否相似?并说明理由;
是否相似?并说明理由;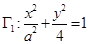
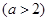 与椭圆
与椭圆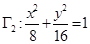 相似,求
相似,求 的值;
的值;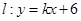 与(2)中的椭圆
与(2)中的椭圆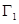 交于
交于 两点,试探究:在椭圆
两点,试探究:在椭圆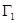 上是否存在异于
上是否存在异于 的定点
的定点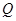 ,使得直线
,使得直线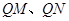 的斜率之积为定值?若存在,求出定点
的斜率之积为定值?若存在,求出定点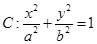
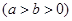 的离心率为
的离心率为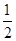 ,其左焦点到点
,其左焦点到点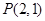 的距离为
的距离为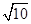 .
. 的标准方程;
的标准方程;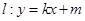 与椭圆
与椭圆 两点(
两点(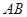 为直径的圆过椭圆
为直径的圆过椭圆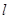 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.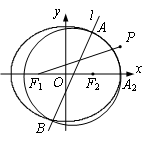
 ,椭圆上第一象限内的点P满足PF1⊥PF2,且△PF1F2的面积为1.
,椭圆上第一象限内的点P满足PF1⊥PF2,且△PF1F2的面积为1.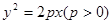 的焦点为F,点A(0,2). 若线段FA的中点B在抛物线上,则B到该抛物线准线的距离为________.
的焦点为F,点A(0,2). 若线段FA的中点B在抛物线上,则B到该抛物线准线的距离为________.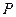 是双曲线
是双曲线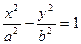 上除顶点外的任意一点,
上除顶点外的任意一点,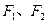 分别为左、右焦点,
分别为左、右焦点,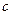 为半焦距,
为半焦距, 的内切圆与
的内切圆与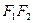 切于点
切于点 ,则
,则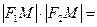 .
. 的离心率为
的离心率为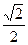 ,若直线
,若直线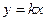 与其一个交点的横坐标为
与其一个交点的横坐标为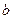 ,则
,则 的值为
的值为