题目内容
定义:我们把椭圆的焦距与长轴的长度之比即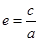 ,叫做椭圆的离心率.若两个椭圆的离心率
,叫做椭圆的离心率.若两个椭圆的离心率 相同,称这两个椭圆相似.
相同,称这两个椭圆相似.
(1)判断椭圆 与椭圆
与椭圆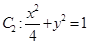 是否相似?并说明理由;
是否相似?并说明理由;
(2)若椭圆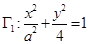
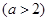 与椭圆
与椭圆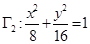 相似,求
相似,求 的值;
的值;
(3)设动直线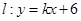 与(2)中的椭圆
与(2)中的椭圆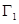 交于
交于 两点,试探究:在椭圆
两点,试探究:在椭圆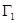 上是否存在异于
上是否存在异于 的定点
的定点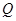 ,使得直线
,使得直线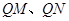 的斜率之积为定值?若存在,求出定点
的斜率之积为定值?若存在,求出定点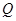 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(1)
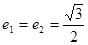 ,
, 相似;(2)
相似;(2)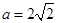 ;(3)
;(3)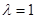 ,
,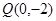 或
或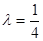 ,
,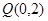 .
.
解析试题分析:(1)掌握好离心率的及时定义即可解决问题;(2)掌握好离心率的及时定义即可解决问题;(3)解析几何中的定点、定值问题是有一定难度的,这种带有探究性问题,通常都假设存在,然后去求,若有解则存在,若无解,则不存在,如何求?如何从一个方程中求出多个字母的值,关键依赖于对题意的正确理解和运算能力,通过这道题我们也能悟出此类题的一般的解题规律.
试题解析:(1)
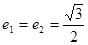 ,
, 相似; 4分
相似; 4分
(2)由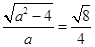 ,得
,得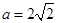 ; 8分
; 8分
(3)设 、
、 、
、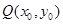 、
、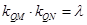 (
( 为常数),将
为常数),将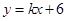 代入
代入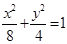 ,整理得
,整理得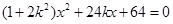 10分
10分
则有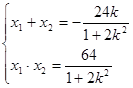 (*)
(*)
由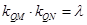 得
得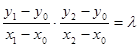 ,即
,即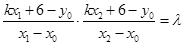
亦即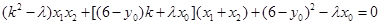 (**)
(**)
将(*)代入(**)整理得: 12分
12分
因为对动直线,总要存在定点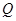 ,所以上式成立与
,所以上式成立与 无关,因此必须有
无关,因此必须有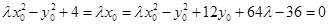 14分
14分
得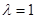 ,
,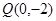 或
或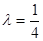 ,
,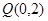 . 16分
. 16分
考点:1.椭圆的方程与性质;2.解析几何中的定点问题的处理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (a>b>0)的离心率为
(a>b>0)的离心率为 ,过原点O斜率为1的直线与椭圆C相交于M,N两点,椭圆右焦点F到直线l的距离为
,过原点O斜率为1的直线与椭圆C相交于M,N两点,椭圆右焦点F到直线l的距离为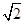 .
.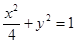 和动圆C2:
和动圆C2: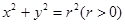 ,直线
,直线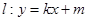 与C1和C2分别有唯一的公共点A和B.
与C1和C2分别有唯一的公共点A和B.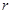 的取值范围;
的取值范围;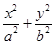 =1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
=1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.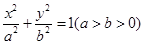 的离心率
的离心率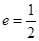 ,右焦点到直线
,右焦点到直线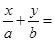 1的距离
1的距离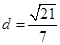 ,O为坐标原点.
,O为坐标原点.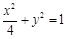 上;
上;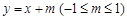 与椭圆W:
与椭圆W: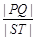 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.
 ,m),A点到抛物线焦点的距离为1.
,m),A点到抛物线焦点的距离为1.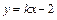 交抛物线
交抛物线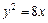 于A,B两点,若AB中点的横坐标是2,则
于A,B两点,若AB中点的横坐标是2,则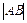 ________.
________.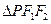 是一个以PF1为底的等腰三角形,
是一个以PF1为底的等腰三角形,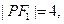 C1的离心率为
C1的离心率为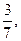 则C2的离心率
则C2的离心率