题目内容
已知抛物线C:y2=2x,O为坐标原点,经过点M(2,0)的直线l交抛物线于A,B两点,P为抛物线C上一点.
(Ⅰ)若直线l垂直于x轴,求|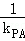 ﹣
﹣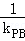 |的值;
|的值;
(Ⅱ)求三角形OAB的面积S的取值范围.
(Ⅰ)2;(Ⅱ)[4,+∞)
解析试题分析:(Ⅰ)若直线l垂直于x轴,交抛物线于(2,2)或(2,-2)不妨设A(2,2),B(2,﹣2),P(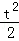 ,t),利用斜率计算公式求得|
,t),利用斜率计算公式求得|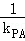 ﹣
﹣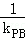 |=2;(Ⅱ)设l:x=ky+2,代入y2=2x中,可得y2﹣2ky﹣4=0
|=2;(Ⅱ)设l:x=ky+2,代入y2=2x中,可得y2﹣2ky﹣4=0
利用弦长公式求得|AB|=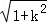 •
•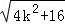 ,三角形OAB的面积S=
,三角形OAB的面积S=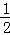 •
•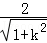 •
•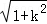 •
•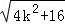 =2
=2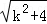 ≥4,三角形OAB的面积S的取值范围为[4,+∞).
≥4,三角形OAB的面积S的取值范围为[4,+∞).
试题解析:(Ⅰ)不妨设A(2,2),B(2,﹣2),P(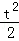 ,t),则
,t),则
|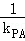 ﹣
﹣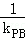 |=|
|=|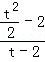 ﹣
﹣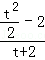 |=2;
|=2;
(Ⅱ)设l:x=ky+2,代入y2=2x中,可得y2﹣2ky﹣4=0
设点A(x1,y1),B(x2,y2),则y1+y2=2k,y1y2=﹣4,
∴|AB|=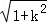 •
•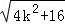 ,
,
∴三角形OAB的面积S=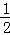 •
•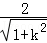 •
•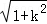 •
•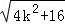 =2
=2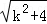 ≥4,
≥4,
∴三角形OAB的面积S的取值范围为[4,+∞).
考点:1.直线的斜率;2.韦达定理与弦长公式;3.直线与抛物线的位置关系

练习册系列答案
相关题目
 (a>b>0)的离心率为
(a>b>0)的离心率为 ,过原点O斜率为1的直线与椭圆C相交于M,N两点,椭圆右焦点F到直线l的距离为
,过原点O斜率为1的直线与椭圆C相交于M,N两点,椭圆右焦点F到直线l的距离为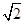 .
.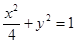 和动圆C2:
和动圆C2: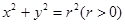 ,直线
,直线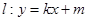 与C1和C2分别有唯一的公共点A和B.
与C1和C2分别有唯一的公共点A和B.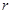 的取值范围;
的取值范围;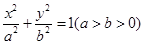 的离心率
的离心率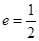 ,右焦点到直线
,右焦点到直线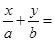 1的距离
1的距离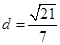 ,O为坐标原点.
,O为坐标原点.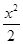 -y2=1的左、右顶点分别为A1,A2,点P(x1,y1),Q(x1,-y1)是双曲线上不同的两个动点.求直线A1P与A2Q交点的轨迹E的方程.
-y2=1的左、右顶点分别为A1,A2,点P(x1,y1),Q(x1,-y1)是双曲线上不同的两个动点.求直线A1P与A2Q交点的轨迹E的方程.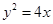 的焦点为
的焦点为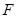 ,准线与
,准线与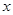 轴的交点为
轴的交点为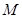 ,
,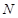 为抛物线上的一点,则满足
为抛物线上的一点,则满足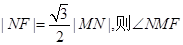 = 。
= 。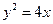 的焦点为圆心,半径为2的圆的标准方程为
的焦点为圆心,半径为2的圆的标准方程为 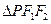 是一个以PF1为底的等腰三角形,
是一个以PF1为底的等腰三角形,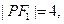 C1的离心率为
C1的离心率为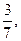 则C2的离心率
则C2的离心率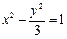 的左顶点为
的左顶点为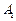 ,右焦点为
,右焦点为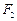 ,
, 为双曲线右支上一点,则
为双曲线右支上一点,则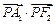 最小值为 _________ .
最小值为 _________ .