题目内容
已知椭圆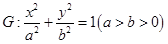 过
过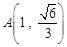 和点
和点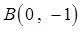 .
.
(1)求椭圆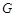 的方程;
的方程;
(2)设过点 的直线
的直线 与椭圆
与椭圆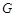 交于
交于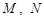 两点,且
两点,且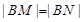 ,求直线
,求直线 的方程.
的方程.
(1)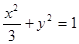 ;(2)
;(2)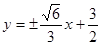 .
.
解析试题分析:(1)由已知将已知两点的坐标代入椭圆G的方程中,可得到关于的方程组,解此方程组就可求得的值,进而就可写出椭圆G的方程.(2)首先注意到由题意可得到直线 的斜率
的斜率 存在,且
存在,且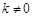 .从而可用斜截式设出直线
.从而可用斜截式设出直线 的方程,代入椭圆G的方程消元得到一个一元二次方程,则此方程一定有两个不同的解,所以
的方程,代入椭圆G的方程消元得到一个一元二次方程,则此方程一定有两个不同的解,所以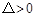 ,可得到
,可得到 的取值范围;再由
的取值范围;再由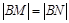 ,得到
,得到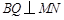 ,结合韦达定理可用
,结合韦达定理可用 的代数式表示出线段MN的中点的坐标,然后由
的代数式表示出线段MN的中点的坐标,然后由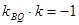 就可求出
就可求出 的值,从而求得直线
的值,从而求得直线 的方程.
的方程.
试题解析:(1)因为椭圆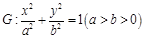 过点
过点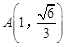 和点
和点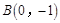 .
.
所以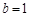 ,由
,由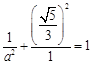 ,得
,得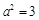 .
.
所以椭圆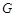 的方程为
的方程为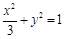 4分
4分
(2)显然直线 的斜率
的斜率 存在,且
存在,且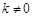 .设直线
.设直线 的方程为
的方程为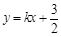 .
.
由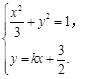 消去
消去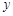 并整理得
并整理得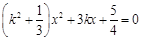 , 5分
, 5分
由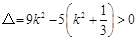 ,
,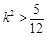 7分
7分
设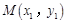 ,
,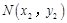 ,
,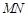 中点为
中点为 ,
,
得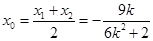 ,
,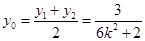 8分
8分
由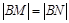 ,知
,知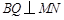 ,
,
所以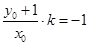 ,即
,即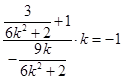 .
.
化简得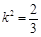 ,满足
,满足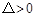 .所以
.所以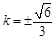 12分
12分
因此直线 的方程为
的方程为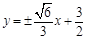 14分
14分
考点:1.椭圆的的方程;2.直线与椭圆的位置关系.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
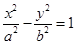 的离心率为
的离心率为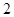 ,它的一个焦点与抛物线
,它的一个焦点与抛物线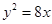 的焦点相同,那么双曲线的焦点坐标为______;渐近线方程为_______.
的焦点相同,那么双曲线的焦点坐标为______;渐近线方程为_______. (a>b>0)的离心率为
(a>b>0)的离心率为 ,过原点O斜率为1的直线与椭圆C相交于M,N两点,椭圆右焦点F到直线l的距离为
,过原点O斜率为1的直线与椭圆C相交于M,N两点,椭圆右焦点F到直线l的距离为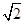 .
. 的焦点为F2,点F1与F2关于坐标原点对称,直线m垂直于x轴(垂足为T),与抛物线交于不同的两点P,Q且
的焦点为F2,点F1与F2关于坐标原点对称,直线m垂直于x轴(垂足为T),与抛物线交于不同的两点P,Q且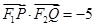 .
.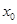 ;
;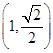 .
.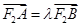 ,若
,若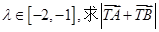 的取值范围.
的取值范围.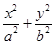 =1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
=1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.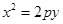 的焦点为F,
的焦点为F,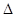 ABQ的三个顶点都在抛物线C上,点M为AB的中点,
ABQ的三个顶点都在抛物线C上,点M为AB的中点,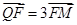 .(1)若M
.(1)若M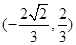 ,求抛物线C方程;(2)若
,求抛物线C方程;(2)若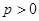 的常数,试求线段
的常数,试求线段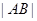 长的最大值.
长的最大值.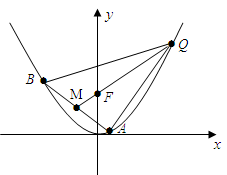
 +
+ =1(a>b>0)的左、右顶点,(1,)为椭圆上一点,椭圆长半轴长等于焦距.
=1(a>b>0)的左、右顶点,(1,)为椭圆上一点,椭圆长半轴长等于焦距.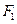 ,
,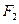 为双曲线左,右焦点,以双曲线右支上任意一点P为圆心,以
为双曲线左,右焦点,以双曲线右支上任意一点P为圆心,以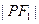 为半径的圆与以
为半径的圆与以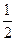
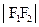 为半径的圆内切,则双曲线两条渐近线的夹角是
为半径的圆内切,则双曲线两条渐近线的夹角是 的准线与x轴交于点Q,若过点Q的直线
的准线与x轴交于点Q,若过点Q的直线 与抛物线有公共点,则直线
与抛物线有公共点,则直线