题目内容
17．不等式|x-1|+|x-3|≥m+1的解为一切实数，求m的范围．分析 由条件利用绝对值的意义求得最小值为2，再由2≥m+1，求得m的范围．
解答 解：|x-1|+|x-3|表示数轴上的x对应点到1、3对应点的距离之和，|x-1|+|x-3|的最小值为2，
故由题意可得2≥m+1，求得m≤1，故m的范围为（-∞，1]．
点评 本题主要考查绝对值的意义，函数的恒成立问题，求函数的最值，属于基础题．
练习册系列答案
相关题目
7．
如图是一个空间几何体的三视图，该几何体的外接球的体积为（ ）
如图是一个空间几何体的三视图，该几何体的外接球的体积为（ ）| A． | 8$\sqrt{2}$ | B． | $\frac{8\sqrt{2}π}{3}$ | C． | 4$\sqrt{2}$π | D． | $\frac{16\sqrt{2}π}{3}$ |
5．在△ABC中，AB=3，BC=$\sqrt{13}$，AC=4，则AC边上的高等于（ ）
| A． | $\frac{3}{2}$$\sqrt{3}$ | B． | $\frac{3}{2}$$\sqrt{2}$ | C． | 3 | D． | 3$\sqrt{3}$ |
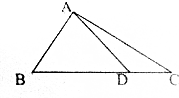已知在△ABC中，点D在BC上，且满足$\overrightarrow{BD}$=3$\overrightarrow{DC}$，若$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$，则x+y=1．
19．设f′（x）是f（x）的导函数，f″（x）是f′（x）的导函数，若函数f（x）在区间I上恒有f″（x）≥0，则称f（x）是区间I上的凸函数，则下列函数在[-1，1]上是凸函数的是（ ）
| A． | f（x）=sinx | B． | f（x）=-cosx | C． | f（x）=x3-x | D． | f（x）=-ex |
海上某货轮在A处看灯塔B在货轮的北偏东75°，距离为12$\sqrt{6}$海里；在A处看灯塔C在货轮的北偏西30°，距离为8$\sqrt{3}$海里；货轮向正北由A处行驶到D处时看灯塔B在货轮的北偏东120°．