题目内容
7. 如图是一个空间几何体的三视图,该几何体的外接球的体积为( )
如图是一个空间几何体的三视图,该几何体的外接球的体积为( )| A. | 8$\sqrt{2}$ | B. | $\frac{8\sqrt{2}π}{3}$ | C. | 4$\sqrt{2}$π | D. | $\frac{16\sqrt{2}π}{3}$ |
分析 根据几何体的三视图,得出该几何体是底面为等腰直角三角形,高为2的直三棱锥;
画出图形,求出该三棱锥外接球的直径,再求外接球的体积.
解答 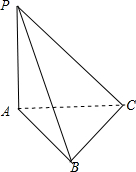 解:根据几何体的三视图,得;
解:根据几何体的三视图,得;
该几何体是底面为等腰直角三角形,高为2的直三棱锥;
如图所示,
PA⊥AB,PA⊥AC,且AB∩AC=A,
∴PA⊥平面ABC,
又AB⊥BC,
∴PC是三棱锥P-ABC外接球的直径;
又PC=$\sqrt{{PA}^{2}{+AC}^{2}}$=$\sqrt{{2}^{2}{+2}^{2}}$=2$\sqrt{2}$,
∴该外接球的半径为$\frac{1}{2}$PC=$\sqrt{2}$,
外接球的体积为$\frac{4}{3}$π•${(\sqrt{2})}^{3}$=$\frac{8\sqrt{2}}{3}$π.
故选:B.
点评 本题考查了空间几何体三视图的应用问题,也考查了空间想象能力与计算能力,是基础题目.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
18.从集合A={1,3,5,7,9}和集合B={2,4,6,8}中各取一个数,那么这两个数之和除3余1的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{10}$ |
15.某几何体三视图如图(单位;cm),则该几何体的体积是( )
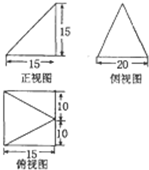

| A. | 1500cm3 | B. | 1025cm3 | C. | 625cm3 | D. | 1200cm3 |
2.在复平面内,复数$\frac{i}{1+i}$+(1+$\sqrt{3}$i)2的共轭复数对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
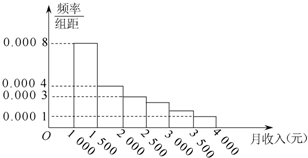 如图是某市有关部门根据该市干部的月收入情况,作抽样调查后画出的样本频率分布直方图.已知图中第一组的频数为4000,请根据该图提供的信息 (图中每组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)),回答:
如图是某市有关部门根据该市干部的月收入情况,作抽样调查后画出的样本频率分布直方图.已知图中第一组的频数为4000,请根据该图提供的信息 (图中每组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)),回答: