题目内容
5.在△ABC中,AB=3,BC=$\sqrt{13}$,AC=4,则AC边上的高等于( )| A. | $\frac{3}{2}$$\sqrt{3}$ | B. | $\frac{3}{2}$$\sqrt{2}$ | C. | 3 | D. | 3$\sqrt{3}$ |
分析 根据三角形的三边长,利用余弦定理求出cosA的值,由A的范围,求出A的度数,然后由AB,AC以及sinA的值,利用三角形的面积公式求出△ABC的面积S,设出AC边上的高,利用三角形的面积公式S=$\frac{1}{2}$b•h,列出关于h的方程,求出方程的解即可得到AC边上的高.
解答 解:设BC=b,AB=c,AC=b,由AB=3,BC=$\sqrt{13}$,AC=4,
根据余弦定理得:
cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{16+9-13}{2×4×3}$=$\frac{1}{2}$,又A∈(0,π),
∴∠A=60°,
∴S△ABC=$\frac{1}{2}$bcsinA=3$\sqrt{3}$,
设AC边上的高为h,
则S△ABC=$\frac{1}{2}$bh=$\frac{1}{2}$×4h=3$\sqrt{3}$,解得h=$\frac{3\sqrt{3}}{2}$,
故选:A.
点评 本题的关键是求出A的值,利用三角形的面积公式列出关于h的方程.要求学生熟练掌握余弦定理及三角形的面积公式,属于中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
15.某几何体三视图如图(单位;cm),则该几何体的体积是( )
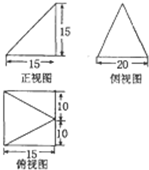

| A. | 1500cm3 | B. | 1025cm3 | C. | 625cm3 | D. | 1200cm3 |
7.下列选项中,说法正确的是( )
| A. | 若命题“p∨q”为真命题,则命题p和命题q均为真命题 | |
| B. | am2<bm2是a<b的必要不充分条件 | |
| C. | x=2kπ+$\frac{π}{4}$(k∈Z)是(-sinx)′=(cosx)′的充要条件 | |
| D. | 命题“若{$\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{b}$+$\overrightarrow{c}$,$\overrightarrow{c}$+$\overrightarrow{a}$}构成空间的一个基底,则{$\overrightarrow{a}$,$\overrightarrow{b}$$\overrightarrow{c}$}构成空间的一个基底”的否命题为真命题 |