题目内容
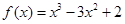 在区间
在区间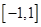 上的最大值是
上的最大值是 2
试题分析:求出函数的导函数,令导函数为0,求出根,判断根是否在定义域内,判断根左右两边的导函数符号,求出最值。
f′(x)=3x2-6x=3x(x-2)令f′(x)=0得x=0或x=2(舍)当-1<x<0时,f′(x)>0;当0<x<1时,f′(x)<0所以当x=0时,函数取得极大值即最大值所以f(x)的最大值为2,故答案为2
点评:解决该试题的关键是求函数的最值,一般先求出函数的极值,再求出区间的端点值,选出最值

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 。
。 的单调区间;
的单调区间;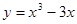 上一点
上一点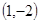 的切线方程。
的切线方程。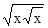 的导数为_______________
的导数为_______________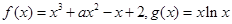
 的单调递减区间为
的单调递减区间为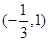 ,求函数
,求函数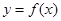 的图像过点
的图像过点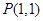 的切线方程;
的切线方程;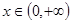 ,
, 恒成立,求实数
恒成立,求实数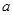 的取值范围.
的取值范围. 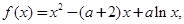 其中常数
其中常数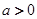 .
.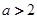 时,求函数
时,求函数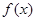 的单调递增区间;
的单调递增区间;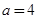 时,若函数
时,若函数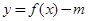 有三个不同的零点,求m的取值范围;
有三个不同的零点,求m的取值范围;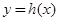 在点
在点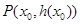 处的切线方程为
处的切线方程为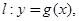 当
当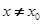 时,若
时,若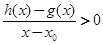 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数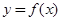 是否存在“类对称点”,若存在,请最少求出一个“类对称点”的横坐标;若不存在,说明理由.
是否存在“类对称点”,若存在,请最少求出一个“类对称点”的横坐标;若不存在,说明理由.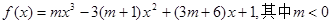 。
。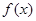 的单调增区间是(0,1)求m的值。
的单调增区间是(0,1)求m的值。 时,函数
时,函数 的图象上任意一点的切线斜率恒大于3m,求m的取值范围。
的图象上任意一点的切线斜率恒大于3m,求m的取值范围。 y=x(x+2)所围成的封闭图形的面积等于
y=x(x+2)所围成的封闭图形的面积等于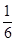
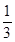
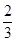
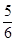
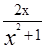 - 2的极值.
- 2的极值.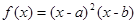 (
( ).
).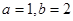 时,求曲线
时,求曲线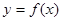 在点
在点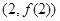 处的切线方程;
处的切线方程; 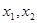 是
是 的两个极值点,
的两个极值点,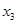 是
是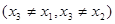 .证明:存在实数
.证明:存在实数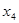 ,使得
,使得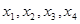 按某种顺序排列后构成等差数列,并求
按某种顺序排列后构成等差数列,并求