题目内容
直线y=x与抛物线 y=x(x+2)所围成的封闭图形的面积等于
y=x(x+2)所围成的封闭图形的面积等于
 y=x(x+2)所围成的封闭图形的面积等于
y=x(x+2)所围成的封闭图形的面积等于A.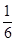 | B.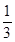 | C.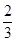 | D.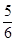 |
A
试题分析:先联立方程,组成方程组,求得交点坐标,可得被积区间,再用定积分表示出曲线y=x2+2x与直线y=x所围成的封闭图形的面积,即可求得结论.y=x与y=x(x+2)联立方程组得到x=-1,y=-1,或x=0,y=0,那可可知直线y=x与抛物线
 y=x(x+2)所围成的封闭图形的面积等于
y=x(x+2)所围成的封闭图形的面积等于S=
 ,故选A
,故选A点评:解决该试题的关键是利用定积分求面积,确定被积区间及被积函数,以及被积函数的原函数的问题,进而得到求解。

练习册系列答案
相关题目
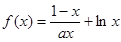
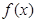 在
在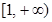 上为增函数,求正实数
上为增函数,求正实数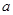 的取值范围;
的取值范围;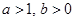 ,求证:
,求证: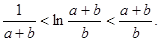
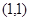 处的切线方程为________________.
处的切线方程为________________.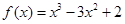 在区间
在区间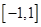 上的最大值是
上的最大值是 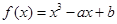 外的点A(1,0)作曲线C的切线恰有两条,
外的点A(1,0)作曲线C的切线恰有两条,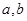 满足的等量关系;
满足的等量关系;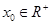 ,使
,使 成立,求
成立,求 的取值范围.
的取值范围.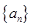 的前
的前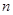 项和为
项和为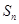 ,函数
,函数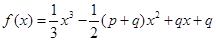 ,
,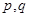 均为常数,且
均为常数,且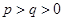 ),当
),当 时,函数
时,函数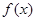 取得极小值.
取得极小值.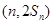
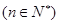 均在函数
均在函数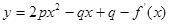 的图像上(其中
的图像上(其中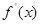 是
是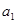 的值;
的值;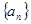 的通项公式.
的通项公式.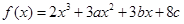 在
在 及
及 时取得极值.
时取得极值. 的值;
的值;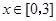 ,都有
,都有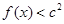 成立,求c的取值范围.
成立,求c的取值范围.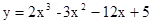 在
在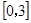 上的最大值和最小值分别是
上的最大值和最小值分别是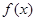 是最小正周期为
是最小正周期为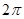 的偶函数,
的偶函数,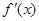 是
是 时,
时,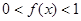 ;当
;当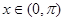 且
且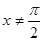 时 ,
时 ,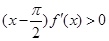 ,则函数
,则函数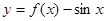 在
在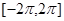 上的零点个数为( )
上的零点个数为( )