题目内容
根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示
(Ⅰ)求上图中 的值;
的值;
(Ⅱ)甲队员进行一次射击,求命中环数大于7环的概率(频率当作概率使用);
(Ⅲ)由上图判断甲、乙两名队员中,哪一名队员的射击成绩更稳定(结论不需证明).
(Ⅰ) ;(Ⅱ)
;(Ⅱ)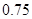 ;(Ⅲ)甲队员的射击成绩更稳定
;(Ⅲ)甲队员的射击成绩更稳定
解析试题分析:(Ⅰ)由频率和为1可求 的值。(Ⅱ)环数大于7环包含环数为8环、9环、10环三个基本事件,而这三个事件两两互斥,所以命中环数大于7环的概率为三个事件概率的和。(Ⅲ)甲队员的射击成绩较集中、波动较小,相对稳定。
的值。(Ⅱ)环数大于7环包含环数为8环、9环、10环三个基本事件,而这三个事件两两互斥,所以命中环数大于7环的概率为三个事件概率的和。(Ⅲ)甲队员的射击成绩较集中、波动较小,相对稳定。
试题解析:解:(Ⅰ)由上图可得 ,
,
所以 . 4分
. 4分
(Ⅱ)设事件A为“甲队员射击,命中环数大于7环”,它包含三个两两互斥的事件:甲队员射击,命中环数为8环,9环,10环.
所以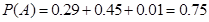 . 9分
. 9分
(Ⅲ)甲队员的射击成绩更稳定. 13分
考点:互斥事件概率及方差的意义。

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
城市公交车的数量太多容易造成资源的浪费,太少又难以满足乘客需求,为此,某市公交公司在某站台的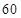 名候车乘客中随机抽取
名候车乘客中随机抽取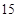 人,将他们的候车时间作为样本分成
人,将他们的候车时间作为样本分成 组,如下表所示(单位:min):
组,如下表所示(单位:min):
| 组别 | 候车时间 | 人数 |
| 一 |  |  |
| 二 |  | 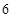 |
| 三 |  |  |
| 四 |  |  |
| 五 |  |  |
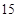 名乘客的平均候车时间;
名乘客的平均候车时间;(2)估计这
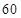 名乘客中候车时间少于
名乘客中候车时间少于 分钟的人数;
分钟的人数;(3)若从上表第三、四组的
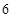 人中选
人中选 人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率. 用分层抽样方法从高中三个年级的相关人员中抽取若干人组成研究小组,有关数据见下表:(单位:人)
| 年级 | 相关人数 | 抽取人数 |
| 高一 | 99 | 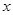 |
| 高二 | 27 | 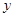 |
| 高三 | 18 | 2 |
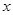 ,
,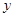 ;
;(Ⅱ)若从高二、高三年级抽取的人中选
 人,求这二人都来自高二年级的概率.
人,求这二人都来自高二年级的概率. 某年青教师近五年内所带班级的数学平均成绩统计数据如下:
年份 年 年 | 2009 | 2010 | 2011 | 2012 | 2013 |
平均成绩 分 分 | 97 | 98 | 103 | 108 | 109 |
 ,并判断它们之间是正相关还是负相关。
,并判断它们之间是正相关还是负相关。(2)利用(1)中所求出的直线方程预测该教师2014年所带班级的数学平均成绩.

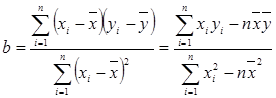


某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
| 分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150) | 总计 |
| 频数 | | | | b | | |
| 频率 | a | 0.25 | | | | |

(1)求表中a,b的值及分数在[90,100)范围内的学生人数,并估计这次考试全校学生数学成绩的及格率(分数在[90,150)内为及格):
(2)从成绩在[100,130)范围内的学生中随机选4人,
设其中成绩在[100,110)内的人数为X,求X的分布列及数学期望.

 ,求恰有一名同学获得该高校B类资格的概率.
,求恰有一名同学获得该高校B类资格的概率.
