题目内容
用分层抽样方法从高中三个年级的相关人员中抽取若干人组成研究小组,有关数据见下表:(单位:人)
| 年级 | 相关人数 | 抽取人数 |
| 高一 | 99 | 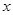 |
| 高二 | 27 | 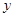 |
| 高三 | 18 | 2 |
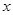 ,
,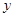 ;
;(Ⅱ)若从高二、高三年级抽取的人中选
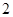 人,求这二人都来自高二年级的概率.
人,求这二人都来自高二年级的概率.
(Ⅰ)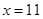 ,
,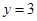 ;(Ⅱ)
;(Ⅱ)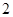 人都来自高二的概率为
人都来自高二的概率为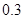 .
.
解析试题分析:(Ⅰ)分层抽样,实质上就是按比例抽样,所以根据比例式 ,即可得
,即可得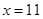 ,
,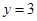 .
.
(Ⅱ)将高二、高三年级抽取的人分别用字母表示出来,可记为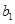 ,
,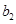 ,
,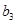 和
和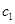 ,
,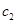 ,然后将所有基本事件(即可能出现的结果)一一列出,数出都来自高二年级的个数,由古典概型的概率公式即得.
,然后将所有基本事件(即可能出现的结果)一一列出,数出都来自高二年级的个数,由古典概型的概率公式即得.
试题解析:(Ⅰ)由题意可得  ,所以
,所以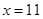 ,
,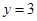 . 4分
. 4分
(Ⅱ)记从高二年级抽取的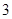 人为
人为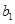 ,
,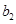 ,
,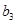 ,从高三年级抽取的
,从高三年级抽取的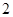 人为
人为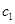 ,
,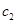 ,
,
则从这两个年级中抽取的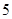 人中选
人中选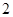 人的基本事件有:
人的基本事件有: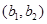 ,
,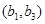 ,
,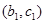 ,
,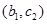 ,
,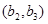 ,
,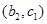 ,
,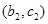 ,
,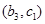 ,
,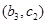 ,
,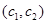 共
共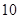 种. 8分
种. 8分
设选中的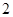 人都来自高二的事件为
人都来自高二的事件为 ,
,
则 包含的基本事件有:
包含的基本事件有: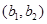 ,
,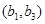 ,
,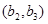 共
共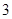 种. 11分
种. 11分
因此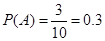 .
.
故选中的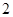 人都来自高二的概率为
人都来自高二的概率为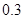 . 13分
. 13分
考点:1、分层抽样;2、古典概型.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关,随机抽取了55名市民,得到数据如下表:
| | 喜欢 | 不喜欢[来源:学科网ZXXK] | 合计 |
| 大于40岁 | 20 | 5 | 25 |
| 20岁至40岁 | 10 | 20 | 30 |
| 合计 | 30 | 25 | 55 |
(Ⅱ)用分层抽样的方法从喜欢“人文景观”景点的市民中随机抽取6人作进一步调查,将这6位市民作为一个样本,从中任选2人,求恰有1位“大于40岁”的市民和1位“20岁至40岁”的市民的概率.
下面的临界值表供参考:
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中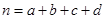 )
) 
 的值;
的值;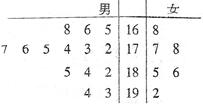
 人,对他们进行年龄状况和受教育情况(只有本科和研究生两类)的调查,其结果如图:
人,对他们进行年龄状况和受教育情况(只有本科和研究生两类)的调查,其结果如图:
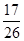 ,求
,求 的值;
的值;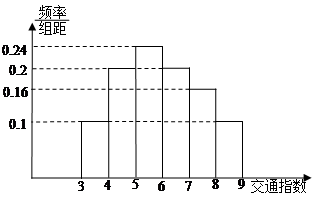
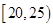 ,第2组
,第2组 ,第3组
,第3组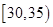 ,第4组
,第4组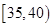 ,第5组
,第5组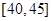 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
