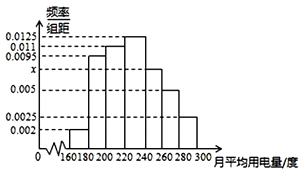
题目内容
【题目】关于函数f（x）=sin （2x﹣ 
）（x∈R），给出下列三个结论： ①对于任意的x∈R，都有f（x）=cos （2x﹣ 
）；
②对于任意的x∈in R，都有f（x+ 
）=f（x﹣ ）；
③对于任意的x∈R，都有f（ 
﹣x）=f（ +x）．
其中，全部正确结论的序号是 ．
【答案】①②③
【解析】解：①f（x）=cos[ 
﹣（2x﹣ 
）]=cos（ 
﹣2x）=cos（2x﹣ ），故①正确，②f（x+ ）=sin[2（x+ ）﹣ ）]=﹣sin（2x﹣ ）]，f（x﹣ ）=sin[2（x﹣ ）﹣ ）]=﹣sin（2x﹣ ），则f（x+ ）=f（x﹣ ）故②正确③f（ 
）=sin（2× ﹣ ）=sin =1为最大值，故x= 是函数的对称轴，故③正确，所以答案是：①②③．
【题目】已知函数f（x）的定义域为[﹣1，5]，部分对应值如表，
x | ﹣1 | 0 | 4 |
f（x） | 1 | 2 | 2 |
f（x）的导函数y=f′（x）的图象（该图象关于（2，0）中心对称） 如图所示．
下列关于f（x）的命题：
①函数f（x）的极大值点为 0与4；
②函数f（x）在[0，2]上是减函数；
③函数y=f（x）﹣a零点的个数可能为0、1、2、3、4个；
④如果当时x∈[﹣1，t]，f（x）的最大值是2，那么t的最大值为5；．
⑤函数f（x）的图象在a=1是上凸的
其中一定正确命题的序号是 ．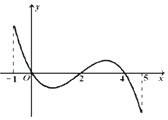 
【题目】一台机器按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产有缺点零件的多少，随机器的运转的速度而变化，具有线性相关关系，下表为抽样试验的结果：
转速x（转/秒） | 8 | 10 | 12 | 14 | 16 |
每小时生产有缺点的零件数y（件） | 5 | 7 | 8 | 9 | 11 |
参考公式： 
， 
= 
= 
．
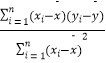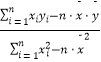（1）如果y对x有线性相关关系，求回归方程；
（2）若实际生产中，允许每小时生产的产品中有缺点的零件最多有10个，那么机器的运转速度应控制在设么范围内？
