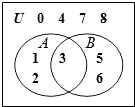
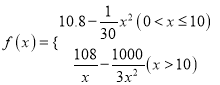题目内容
【题目】一台机器按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产有缺点零件的多少，随机器的运转的速度而变化，具有线性相关关系，下表为抽样试验的结果：
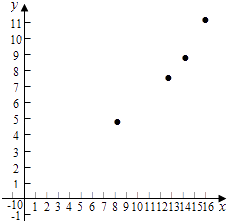
转速x（转/秒） | 8 | 10 | 12 | 14 | 16 |
每小时生产有缺点的零件数y（件） | 5 | 7 | 8 | 9 | 11 |
参考公式： 
， 
= 
= 
．
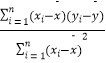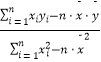（1）如果y对x有线性相关关系，求回归方程；
（2）若实际生产中，允许每小时生产的产品中有缺点的零件最多有10个，那么机器的运转速度应控制在设么范围内？
【答案】
（1）解： 
=12， 
=8，
40+70+96+126+176﹣5×12×8=28，
64+100+144+196+256﹣5×144=40，
∴b=0.7，a=8﹣0.7×12=﹣0.4
∴回归直线方程为：y=0.7x﹣0.4
（2）解：由上一问可知0.7x﹣0.4≤10，
解得x≤14.85．
【解析】（1）先做出横标和纵标的平均数，做出利用最小二乘法求线性回归方程的系数的量，做出系数，求出a，写出线性回归方程．（2）根据上一问做出的线性回归方程，使得函数值小于或等于10，解出不等式．
亮点激活精编提优100分大试卷系列答案
【题目】某公司为了了解一年内的用水情况，抽取了10天的用水量如表所示：
天数 | 1 | 1 | 1 | 2 | 2 | 1 | 2 |
用水量/吨 | 22 | 38 | 40 | 41 | 44 | 50 | 95 |
（Ⅰ）在这10天中，该公司用水量的平均数是多少？每天用水量的中位数是多少？
（Ⅱ）你认为应该用平均数和中位数中的哪一个数来描述该公司每天的用水量？
【题目】已知f（x+y）=f（x）+f（y）且f（1）=2，则f（1）+f（2）+…+f（n）不能等于（ ）
A.f（1）+2f（1）+…+nf（1）
B.f（ 
）
C.n（n+1）
D.n（n+1）f（1）
【题目】如表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量x（吨）与相应的生产能耗y（吨）的几组对应数据，根据表提供的数据，求出y关于x的线性回归方程为 
=0.7x+0.35，则下列结论错误的是（ ）
x | 3 | 4 | 5 | 6 |
y | 2.5 | t | 4 | 4.5 |
A.产品的生产能耗与产量呈正相关
B.t的取值必定是3.15
C.回归直线一定过点（4，5，3，5）
D.A产品每多生产1吨，则相应的生产能耗约增加0.7吨
