题目内容
【题目】用系统抽样方法从960人中抽取32人做问卷调查为此将他们随机编号为1,2,…,960,分组后在第一组采用简单随机抽样的方法抽到的号码为9,若抽到的32人中,编号落入区间[1,450]的人做问卷A,编号落人区间[451,750]的人做问卷B,其余的人做问卷C,则抽到的人中,做问卷C的人数为 .
【答案】7
【解析】解:∵960÷32=30, ∴由题意可得抽到的号码构成以9为首项、以30为公差的等差数列,
且此等差数列的通项公式为an=9+(n﹣1)30=30n﹣21.
落人区间[751,960]的人做问卷C,
由 751≤30n﹣21≤960,
即772≤30n≤981
解得 ![]() ≤n≤
≤n≤ ![]() .
.
再由n为正整数可得 26≤n≤32,
∴做问卷C的人数为32﹣26+1=7,
所以答案是:7
【考点精析】利用系统抽样方法对题目进行判断即可得到答案,需要熟知把总体的单位进行排序,再计算出抽样距离,然后按照这一固定的抽样距离抽取样本;第一个样本采用简单随机抽样的办法抽取.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案【题目】某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如表:
API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(1)若某企业每天由空气污染造成的经济损失S(单位:元)与空气质量指数API(记为ω)的关系式为: S= 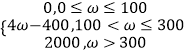 ,试估计在本年内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
,试估计在本年内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
(2)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面2×2列联表,并判断能否有95%的把握认为该市本年空气重度污染与供暖有关? 附:
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
k2= ![]()
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |