题目内容
(本题满分12分)在数列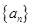 中,
中,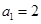 ,
,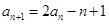 (
(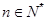 ),数列
),数列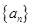 的前
的前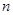 项和为
项和为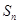 。(1)证明:数列
。(1)证明:数列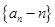 是等比数列,并求数列
是等比数列,并求数列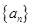 的通项公式;(2)求
的通项公式;(2)求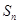 ;(3)证明:
;(3)证明: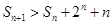 。
。
(1)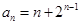 。(2)
。(2)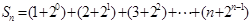
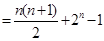 。
。
(3)见解析。
解析试题分析:(1)因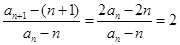 ,故数列
,故数列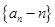 是公比为2的等比数列(1分)。
是公比为2的等比数列(1分)。
又因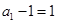 (2分),故
(2分),故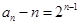 (3分),
(3分),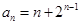 (4分)。
(4分)。
(2)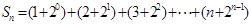 (5分)
(5分) (6分)
(6分)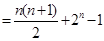 (8分)。
(8分)。
(3)由(2):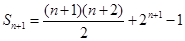 (9分),
(9分),
故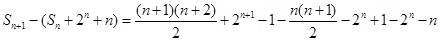 (10分)
(10分)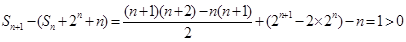 (11分),故
(11分),故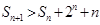 (12分)。
(12分)。
考点:本题考查等比数列的定义、通项公式、分组求和法和用作差法证明不等式。
点评:是一道不错的综合题。等比数列与不等式综合在一起考查。

练习册系列答案
相关题目
数列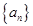 中,
中,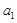 =2,
=2, ,则
,则 =( ).
=( ).
| A.2+ln n | B.2+ (n-1) ln n | C.2+ n ln n | D.1+n+ln n |
设函数 )定义为如下数表,且对任意自然数n均有xn+1=
)定义为如下数表,且对任意自然数n均有xn+1=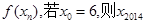 的值为( )
的值为( )
| A.1 | B.2 | C.4 | D.5 |
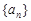 满足:
满足: ,数列
,数列 满足
满足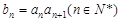 .
.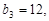 求
求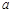 的值及
的值及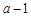 的等比数列,问是否存在正实数
的等比数列,问是否存在正实数 ,使得数列
,使得数列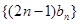 的前
的前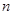 项和
项和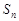 (用n,
(用n,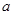 表示).
表示). 满足:
满足: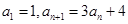 ;
;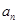 ;
;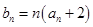 ,求数列
,求数列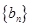 的前
的前 项和为
项和为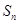 。
。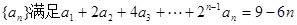 .
.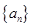 的通项公式;
的通项公式;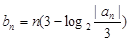 ,探求使
,探求使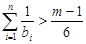 恒成立的
恒成立的 的最大整数值.
的最大整数值.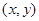 是区域
是区域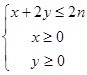 ,(
,(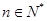 )内的点,目标函数
)内的点,目标函数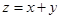 ,
, 的最大值记作
的最大值记作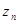 .若数列
.若数列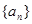 的前
的前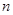 项和为
项和为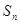 ,
,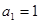 ,且点(
,且点(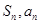 )在直线
)在直线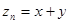 上.
上. 为等比数列;
为等比数列;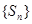 的前
的前 .
.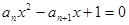 ,
,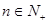 有两根
有两根 和
和 ,且满足
,且满足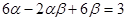 ,
, 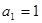
 表示
表示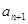 ; (2)证明
; (2)证明 是等比数列;
是等比数列; ,
,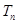 为
为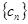 的前n项和,证明
的前n项和,证明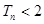 ,(
,(