题目内容
(本小题满分12分)已知数列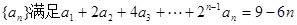 .
.
(1)求数列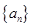 的通项公式;
的通项公式;
(2)设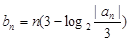 ,探求使
,探求使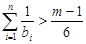 恒成立的
恒成立的 的最大整数值.
的最大整数值.
(1)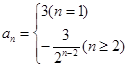 (2)2
(2)2
解析试题分析:(1)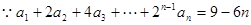 ①
①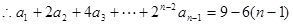 ②
②
①-②得: 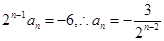 ,
,
当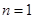 时,由题设得
时,由题设得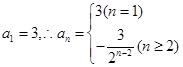 . ……6分
. ……6分
(2)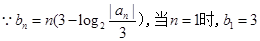 ,
,
当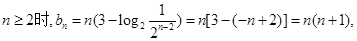
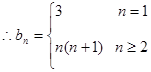 ,
,
设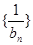 前n项和为
前n项和为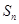 ,
,
当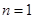 时,
时,  >
>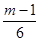 ,得
,得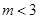 ①
①
当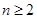 时
时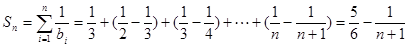 (
(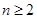 )
)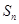 (
(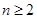 )递增,其最小值为
)递增,其最小值为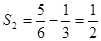 .
.
要使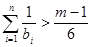 (
(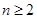 ),
),
只须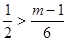 ,即
,即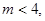 ②
②
综上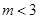 ,
,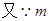 为整数,∴
为整数,∴ 的最大值为2. ……12分
的最大值为2. ……12分
考点:本小题主要考查由数列的递推关系式求通项公式、裂项相消法求数列的前n项和以及利用单调性解决不等式中求参数问题,考查学生的运算求解能力和转化问题的能力.
点评:由递推关系式求通项公式时,一定不要忘记验证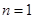 时是否符合;另外,裂项相消法也是一种常考的方法,与错位相减法同样重要,要重点练习.
时是否符合;另外,裂项相消法也是一种常考的方法,与错位相减法同样重要,要重点练习.

练习册系列答案
相关题目
已知数列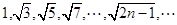 ,则
,则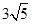 是它的( )
是它的( )
| A.第22项 | B.第23项 | C.第24项 | D.第28项 |
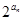 }的前n项和Sn.
}的前n项和Sn.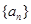 中,
中,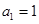 ,
,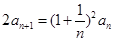 .
. ,求数列
,求数列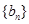 的前
的前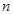 项和
项和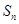 .
.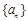 满足:
满足: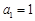 ,
,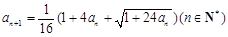 。
。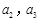 ;
; 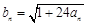 ,求数列
,求数列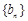 的通项公式;
的通项公式;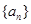 中,
中,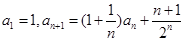 ,
, 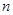 项和
项和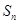
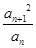 (其中P为非零常数,n∈N *)
(其中P为非零常数,n∈N *)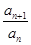 }是不是等比数列?
}是不是等比数列?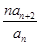 ,Sn为数列{bn}的前n项和,求Sn。
,Sn为数列{bn}的前n项和,求Sn。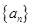 中,
中,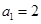 ,
,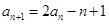 (
(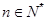 ),数列
),数列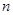 项和为
项和为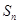 。(1)证明:数列
。(1)证明:数列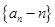 是等比数列,并求数列
是等比数列,并求数列 。
。