题目内容
6.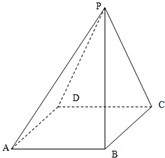 如图:四棱锥P-ABCD中,底面ABCD是边长为2的正方形,平面PCD⊥底面ABCD,且PC=PD=a.
如图:四棱锥P-ABCD中,底面ABCD是边长为2的正方形,平面PCD⊥底面ABCD,且PC=PD=a.(1)求证:PD⊥BC;
(2)当a的值为多少时满足PC⊥平面PAD?并求出此时该四棱锥P-ABCD的体积.
分析 (1)利用平面与平面垂直的性质,可得BC⊥平面PDC,即可证明PD⊥BC;
(2)取CD的中点为O,连接PO,证明PO⊥平面ABCD,由题意可得PC⊥PD,a=$\sqrt{2}$,PO=1,即可求出四棱锥P-ABCD的体积.
解答 (1)证明:∵平面PCD⊥底面ABCD,平面PCD∩平面ABCD=DC,BC⊥DC,
∴BC⊥平面PDC,
∵PD?平面PDC,∴PD⊥BC…(5分)
(2)解:取CD的中点为O,连接PO
∵平面PCD⊥底面ABCD,平面PCD∩平面ABCD=DC,
且PO?平面PCD,PO⊥CD
∴PO⊥平面ABCD…(8分)
由题意可得PC⊥PD,a=$\sqrt{2}$,PO=1,…(10分)
此时该四棱锥的体积为V=$\frac{1}{3}$×22×1=$\frac{4}{3}$…(12分)
点评 本题考查线面垂直,面面垂直,考查几何体体积的计算,考查学生分析解决问题的能力,正确运用面面垂直的性质是关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
17.如图是一个几何体的三视图,则该几何体可能是( )
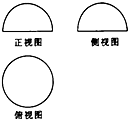

| A. | 半球 | B. | 球 | C. | 圆柱 | D. | 圆锥 |
1.棱长均为4的三棱锥的顶点都在同一个球面上,则该球的表面积为( )
| A. | $\frac{8}{3}π$ | B. | 6π | C. | 16π | D. | 24π |
11.已知{an}的通项an=23-n,则a1a2+a2a3+…+anan+1=( )
| A. | $\frac{32}{3}$(1-4-n) | B. | $\frac{32}{3}$(1-2-n) | C. | 16(1-4-n) | D. | 16(1-2-n) |
18.下列说法中正确的是( )
| A. | 命题“若a>b>0,则$\frac{1}{a}<\frac{1}{b}$”的逆命题是真命题 | |
| B. | 命题p:?x∈R,2x>0,则¬p:?x0∈R,2x0<0 | |
| C. | “a>1,b>1”是“ab>1”成立的充分条件 | |
| D. | “a>b”是“a2>b2”成立的充分不必要条件 |
15.偶函数f(x)=loga|x+b|在(-∞,0)上单调递减,则f(a+1)与f(2-b)的大小关系是( )
| A. | f(a+1)>f(2-b) | B. | f(a+1)=f(2-b) | C. | f(a+1)<f(2-b) | D. | 不能确定 |
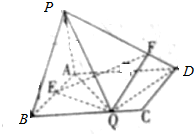 如图所示,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1,E为AB中点,F、Q分别在边PD、BC上,$\overrightarrow{PF}$=λ$\overrightarrow{PD}$,λ∈(0,1),且仅存在唯一一点Q,使得PQ⊥QD.
如图所示,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1,E为AB中点,F、Q分别在边PD、BC上,$\overrightarrow{PF}$=λ$\overrightarrow{PD}$,λ∈(0,1),且仅存在唯一一点Q,使得PQ⊥QD.