题目内容
11．已知{an}的通项an=23-n，则a1a2+a2a3+…+anan+1=（ ）| A． | $\frac{32}{3}$（1-4-n） | B． | $\frac{32}{3}$（1-2-n） | C． | 16（1-4-n） | D． | 16（1-2-n） |
分析 an=23-n，可得anan+1=$\frac{32}{{4}^{n}}$，再利用等比数列的前n项和公式即可得出．
解答 解：∵an=23-n，∴anan+1=23-n•23-（n+1）=25-2n=$\frac{32}{{4}^{n}}$，
∴a1a2+a2a3+…+anan+1=$32（\frac{1}{4}+\frac{1}{{4}^{2}}+…+\frac{1}{{4}^{n}}）$=$32×\frac{\frac{1}{4}（1-\frac{1}{{4}^{n}}）}{1-\frac{1}{4}}$=$\frac{32}{3}（1-{4}^{-n}）$．
故选：A．
点评 本题考查了等比数列的通项公式及其前n项和公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
19．在区间[-3，5]上随机取一个实数a，则使函数f（x）=x2+2ax+4无零点的概率是（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{8}$ |
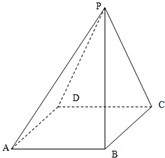如图：四棱锥P-ABCD中，底面ABCD是边长为2的正方形，平面PCD⊥底面ABCD，且PC=PD=a．