题目内容
18.下列说法中正确的是( )| A. | 命题“若a>b>0,则$\frac{1}{a}<\frac{1}{b}$”的逆命题是真命题 | |
| B. | 命题p:?x∈R,2x>0,则¬p:?x0∈R,2x0<0 | |
| C. | “a>1,b>1”是“ab>1”成立的充分条件 | |
| D. | “a>b”是“a2>b2”成立的充分不必要条件 |
分析 A.原命题的逆命题为“若$\frac{1}{a}<\frac{1}{b}$,则a>b>0”,取b=-2,a=-1,即可判断出其逆命题的真假;
B.利用命题的否定定义即可判断出正误;
C.“a>1,b>1”⇒“ab>1”,反之不成立,例如:取a=10,b=$\frac{1}{2}$,即可判断出正误;
D.“a2>b2”?|a|>|b|,即可判断出其正误.
解答 解:A.“若a>b>0,则$\frac{1}{a}<\frac{1}{b}$”的逆命题为“若$\frac{1}{a}<\frac{1}{b}$,则a>b>0”是假命题,取b=-2,a=-1,即可判断出其逆命题是假命题;
B.p:?x∈R,2x>0,则¬p:?x0∈R,2x0≤0,因此不正确;
C.“a>1,b>1”⇒“ab>1”,反之不成立,例如:取a=10,b=$\frac{1}{2}$,满足ab>1,而b<1,因此“a>1,b>1”是“ab>1”成立的充分不必要条件,正确;
D.“a2>b2”?|a|>|b|,因此“a>b”是“a2>b2”成立的既不充分也不必要条件,因此不正确.
故选:C.
点评 本题考查了简易逻辑的判定方法、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
8.已知a,b是空间中两不同直线,α,β是空间中两不同平面,下列命题中正确的是( )
| A. | 若直线a∥b,b?α,则a∥α | B. | 若平面α⊥β,a⊥α,则a∥β | ||
| C. | 若平面α∥β,a?α,b?β,则a∥b | D. | 若a⊥α,b⊥β,a∥b,则α∥β |
9.执行如图所示的程序框图,输出的结果为( )


| A. | 7 | B. | 9 | C. | 11 | D. | 13 |
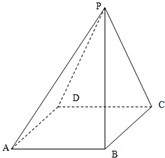 如图:四棱锥P-ABCD中,底面ABCD是边长为2的正方形,平面PCD⊥底面ABCD,且PC=PD=a.
如图:四棱锥P-ABCD中,底面ABCD是边长为2的正方形,平面PCD⊥底面ABCD,且PC=PD=a.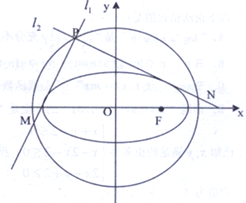 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点F($\sqrt{2}$,0)其短轴上的一个端点到F的距离为$\sqrt{3}$
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点F($\sqrt{2}$,0)其短轴上的一个端点到F的距离为$\sqrt{3}$