Question

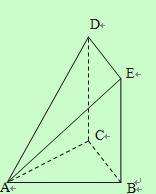
【题目】某设计部门承接一产品包装盒的设计（如图所示），客户除了要求、边的长分别为和外，还特别要求包装盒必需满足：①平面平面；②平面与平面所成的二面角不小于；③包装盒的体积尽可能大．

若设计部门设计出的样品满足：与均为直角且长，矩形的一边长为，请你判断该包装盒的设计是否能符合客户的要求？说明理由．

Answer 1

【答案】满足，理由见解析．

【解析】

假设满足，只需证明满足①、②、③即可．

假设该包装盒的样品设计符合客户的要求．

（1）以下证明满足条件①的要求.

∵四边形为矩形，与均为直角，

∴且∴面，

在矩形中，∥

∴面∴面面

（2）以下证明满足条件②、③的要求.

∵矩形的一边长为，

而直角三角形的斜边长为，∴

设，则，

以为原点，分别为轴的正半轴建立空间直角坐标系，

则，，，

设面的一个法向量为，，

∵

∴，取，则

而平面的一个法向量为，

设面与面所成的二面角为，则，

∴， ∴，

即当时，面与面所成的二面角不小于

又， 由与均为直角知，面，该包装盒可视为四棱锥，

当且仅当，即时，的体积最大，最大值为

而，可以满足面与面所成的二面角不小于的要求，

综上，该包装盒的设计符合客户的要求．