题目内容
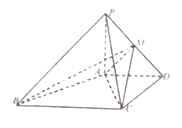
【题目】在平面四边形ABCD中, AB=2,BD=![]() ,AB⊥BC,∠BCD=2∠ABD,△ABD的面积为2.
,AB⊥BC,∠BCD=2∠ABD,△ABD的面积为2.

(1)求AD的长;
(2)求△CBD的面积.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)利用面积公式可以求出sin∠ABD的值,利用同角三角函数的关系求出cos∠ABD的值,利用余弦定理,求出AD的长;
(2)利用AB⊥BC,可以求出以sin∠CBD的大小,利用∠BCD=2∠ABD,可求出sin∠BCD
的大小,通过角之间的关系可以得到所以△CBD为等腰三角形,利用正弦定理,可求出CD的大小,最后利用面积公式求出△CBD的面积.
(1)由已知![]() =
=![]() AB·BD·sin∠ABD=
AB·BD·sin∠ABD=![]() ×2×
×2×![]() ×sin∠ABD=2,
×sin∠ABD=2,
可得sin∠ABD=![]() ,又∠ABD∈
,又∠ABD∈![]() ,所以cos∠ABD=
,所以cos∠ABD=![]() ,
,
在△ABD中,由余弦定理AD2=AB2+BD2-2·AB·BD·cos∠ABD,
可得AD2=5,所以AD=![]() .
.
(2)由AB⊥BC,得∠ABD+∠CBD=![]() ,所以sin∠CBD=cos∠ABD=
,所以sin∠CBD=cos∠ABD=![]() ,
,
又∠BCD=2∠ABD,所以sin∠BCD=2sin∠ABD·cos∠ABD=![]() ,
,
∠BDC=π-∠CBD-∠BCD=π-![]() -2∠ABD=
-2∠ABD=![]() -∠ABD=∠CBD,
-∠ABD=∠CBD,
所以△CBD为等腰三角形,即CB=CD,在△CBD中,由正弦定理![]() ,得CD
,得CD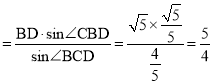 ,
,
所以![]() .
.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
【题目】为考查某种疫苗预防疾病的效果,进行动物实验,得到统计数据如下:
未发病 | 发病 | 总计 | |
未注射疫苗 | 20 |
|
|
注射疫苗 | 30 |
|
|
总计 | 50 | 50 | 100 |
现从所有试验动物中任取一只,取到“注射疫苗”动物的概率为![]() .
.
(1)求![]() 列联表中的数据
列联表中的数据![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)判断疫苗是否有效?
(3)能够有多大把握认为疫苗有效?
(参考公式![]() ,
,![]() )
)
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |