题目内容
将背面相同正面分别标有1、2、3、4的四张卡片洗匀后背面朝上放在桌面上,(1)从中随机的抽取一张卡片,求该卡片正面上的数字是偶数的概率(2)先从中随机的抽取一张卡片(不放回),将该卡片正面上的数字作为十位数字,再随机的抽取一张卡片,将该卡片正面上的数字作为个位数字,则组成的两位数恰好是4的倍数的概率是多少?
(1)
(2)0.5
解析试题分析:(1)根据题意,由于背面相同正面分别标有1、2、3、4的四张卡片洗匀后背面朝上放在桌面上,从中随机的抽取一张卡片,求该卡片正面上的数字不是奇数就是偶数,因此可知是偶数的概率为 -3分
-3分
(2)解:,设组成的两位数恰好是4的倍数的事件为A,由题设知,基本事件有:12,21,13,31,14,41,23,32,24,42,34,43,其总个数为12个,组成的两位数恰好是4的倍数的事件A包含的基本事件的个数为3个,古典概型的概率公式得P(A)=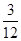
即:P(A)= 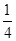 -10分
-10分
考点:古典概型
点评:主要是考查了古典概型概率的计算,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
德阳中学数学竞赛培训共开设有初等代数、初等几何、初等数论和微积分初步共四门课程,要求初等代数、初等几何都要合格,且初等数论和微积分初步至少有一门合格,则能取得参加数学竞赛复赛的资格,现有甲、乙、丙三位同学报名参加数学竞赛培训,每一位同学对这四门课程考试是否合格相互独立,其合格的概率均相同,(见下表),且每一门课程是否合格相互独立,
| 课 程 | 初等代数 | 初等几何 | 初等数论 | 微积分初步 |
| 合格的概率 |  |  |  |  |
(2)记
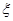 表示三位同学中取得参加数学竞赛复赛的资格的人数,求
表示三位同学中取得参加数学竞赛复赛的资格的人数,求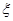 的分布列及期望
的分布列及期望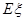 .
. 某普通高中共有教师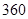 人,分为三个批次参加研修培训,在三个批次中男、女教师人数如下表所示:
人,分为三个批次参加研修培训,在三个批次中男、女教师人数如下表所示:
| | 第一批次 | 第二批次 | 第三批次 |
| 女教师 | 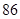 | 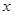 | 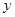 |
| 男教师 | 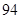 |  | 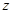 |
已知在全体教师中随机抽取1名,抽到第二、三批次中女教师的概率分别是
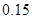 、
、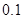 .
.(Ⅰ)求
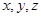 的值;
的值;(Ⅱ)为了调查研修效果,现从三个批次中按
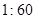 的比例抽取教师进行问卷调查,三个批次被选取的人数分别是多少?
的比例抽取教师进行问卷调查,三个批次被选取的人数分别是多少?(Ⅲ)若从(Ⅱ)中选取的教师中随机选出两名教师进行访谈,求参加访谈的两名教师“分别来自两个批次”的概率.
甲,乙两人进行射击比赛,每人射击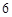 次,他们命中的环数如下表:
次,他们命中的环数如下表:
| 甲 | 5 | 8 | 7 | 9 | 10 | 6 |
| 乙 | 6 | 7 | 4 | 10 | 9 | 9 |
(Ⅱ)把甲6次射击命中的环数看成一个总体,用简单随机抽样方法从中抽取两次命中的环数组成一个样本,求该样本平均数与总体平均数之差的绝对值不超过
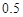 的概率.
的概率. 
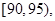
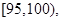
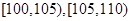 后得到如下图的频率分布直方图.
后得到如下图的频率分布直方图. 的车辆中任抽取2辆,求抽出的2辆车中车速在
的车辆中任抽取2辆,求抽出的2辆车中车速在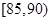 的车辆数
的车辆数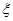 的分布列及数学期望.
的分布列及数学期望.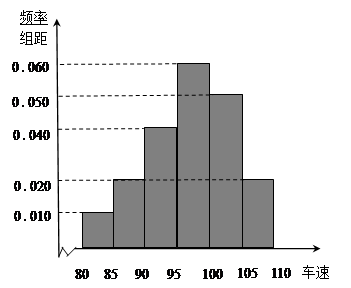
 人,每人回答一个问题,答对者为本队赢得一分,答错得零分。假设甲队中每人答对的概率均为
人,每人回答一个问题,答对者为本队赢得一分,答错得零分。假设甲队中每人答对的概率均为 ,乙队中
,乙队中 且各人正确与否相互之间没有影响.用
且各人正确与否相互之间没有影响.用 表示甲队的总得分.
表示甲队的总得分. 表示“甲、乙两个队总得分之和等于
表示“甲、乙两个队总得分之和等于 表示“甲队总得分大于乙队总得分”这一事件,求
表示“甲队总得分大于乙队总得分”这一事件,求 。
。