题目内容
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机取两个球,求取出的球的编号之和不大于4的概率;
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率.
(1) P=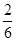 =
=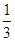 .(2)满足条件n<m+2的事件的概率为
.(2)满足条件n<m+2的事件的概率为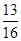 .
.
解析试题分析:(1)从袋中随机取两个球,其一切可能的结果组成的基本事件有1和2,1和3,1和4,2和3,2和4,3和4,共6个.
从袋中取出的球的编号之和不大于4的事件共有1和2,1和3两个.
因此所求事件的概率P=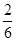 =
=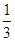 .
.
(2)先从袋中随机取一个球,记下编号为m,放回后,再从袋中随机取一个球,记下编号为n,其一切可能的结果(m,n)有:
(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16个.
又满足条件n≥m+2的事件为(1,3),(1,4),(2,4),共3个.
所以满足条件n≥m+2的事件的概率为P1=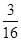 .
.
故满足条件n<m+2的事件的概率为
1-P1=1-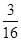 =
=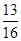 .
.
考点:古典概型概率的计算
点评:中档题,古典概型要求所有结果出现的可能性都相等,强调所有结果中每一结果出现的概率都相同.解决问题的步骤是:计算满足条件的基本事件个数,及基本事件的总个数,然后代入古典概型计算公式进行求解。为防止遗漏,常常利用“树图法”或“坐标法”。

有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排列组成.
| 第一排 | 明文字符 | A | B | C | D |
| 密码字符 | 11 | 12 | 13 | 14 | |
| 第二排 | 明文字符 | E | F | G | H |
| 密码字符 | 21 | 22 | 23 | 24 | |
| 第三排 | 明文字符 | M | N | P | Q |
| 密码字符 | 1 | 2 | 3 | 4 |
(1)求
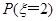 ;
;(2)求随机变量
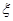 的分布列和数学期望.
的分布列和数学期望. (本小题满分12分)有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成,且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排成一排组成.
| 第一排 | 明文字符 | A | B | C | D |
| 密码字符 | 11 | 12 | 13 | 14 | |
| 第二排 | 明文字符 | E | F | G | H |
| 密码字符 | 21 | 22 | 23 | 24 | |
| 第三排 | 明文字符 | M | N | P | Q |
| 密码字符 | 1 | 2 | 3 | 4 |
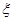 表示密码中不同数字的个数.
表示密码中不同数字的个数.(Ⅰ)求
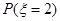 ; (Ⅱ)求随机变量
; (Ⅱ)求随机变量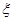 的分布列和它的数学期望.
的分布列和它的数学期望. 为了对某课题进行研究,用分层抽样的方法从 三所高校的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人).
三所高校的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人).
| 高校 | 相关人数 | 抽取人数 |
 | 18 |  |
 | 36 |  |
 | 54 |  |
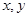 ;
;(2) 若从高校
 抽取的人中选2人作专题发言,求这2人都来自高校
抽取的人中选2人作专题发言,求这2人都来自高校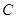 的概率.
的概率. 某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花做垃圾处理.
(Ⅰ)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.
(Ⅱ)花店记录了100 天玫瑰花的日需求量(单位:枝),整理得下表:
| 日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
(ii)若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率.
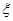 ,求
,求 箱中有3个黑球,6个白球,每个球被取到的概率相同,
箱中有3个黑球,6个白球,每个球被取到的概率相同,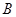 箱中没有球.我们把从
箱中没有球.我们把从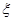 ,求
,求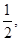 各局比赛的结果都相互独立,第
各局比赛的结果都相互独立,第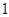 局甲当裁判.
局甲当裁判. 局甲当裁判的概率;
局甲当裁判的概率;