题目内容
节日期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段 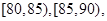
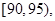
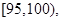
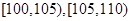 后得到如下图的频率分布直方图.
后得到如下图的频率分布直方图.
(1)此调查公司在采样中,用到的是什么抽样方法?
(2)求这40辆小型车辆车速的众数和中位数的估计值;
(3)若从车速在 的车辆中任抽取2辆,求抽出的2辆车中车速在
的车辆中任抽取2辆,求抽出的2辆车中车速在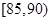 的车辆数
的车辆数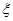 的分布列及数学期望.
的分布列及数学期望.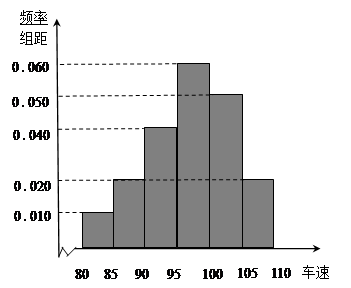
(1)系统抽样;(2)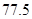 ;(3)
;(3)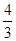 .
.
解析试题分析:(1)根据“某段高速公路的车速(km/h)分成六段”,符合系统抽验的原理;(2)根据中位数的估算公式直接求解;(3)首先明确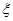 的含义,确定其所有取值,然后利用随机事件的概率求解各概率,最后写出分布列和计算期望.
的含义,确定其所有取值,然后利用随机事件的概率求解各概率,最后写出分布列和计算期望.
试题解析:(1)系统抽样. 2分
(2)众数的估计值为最高的矩形的中点,即众数的估计值等于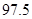 .
.
设图中虚线所对应的车速为 ,则中位数的估计值为:
,则中位数的估计值为:  ,解得
,解得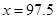 ,
,
即中位数的估计值为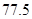 . 6分
. 6分
(3)从图中可知,车速在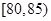 的车辆数为
的车辆数为 (辆),
(辆),
车速在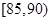 的车辆数为
的车辆数为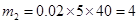 (辆) ,
(辆) ,
∴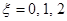 ,
, 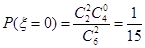 ,
,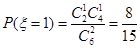 ,
, ,
, 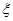 的分布列为
的分布列为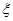
0 1 2 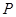
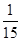
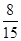
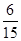
均值 . 12分
. 12分
考点:1.抽样方法;2.中位数;(3)分布列和期望.

 步步高达标卷系列答案
步步高达标卷系列答案为调查乘客的候车情况,公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间(单位:分钟)作为样本分成5组,如下表所示:
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
| 组别 | 候车时间 | 人数 |
| 一 | 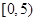 | 2 |
| 二 | 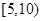 | 6 |
| 三 | 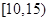 | 4 |
| 四 | 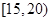 | 2 |
| 五 | 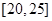 | 1 |
(本小题满分12分)有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成,且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排成一排组成.
| 第一排 | 明文字符 | A | B | C | D |
| 密码字符 | 11 | 12 | 13 | 14 | |
| 第二排 | 明文字符 | E | F | G | H |
| 密码字符 | 21 | 22 | 23 | 24 | |
| 第三排 | 明文字符 | M | N | P | Q |
| 密码字符 | 1 | 2 | 3 | 4 |
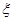 表示密码中不同数字的个数.
表示密码中不同数字的个数.(Ⅰ)求
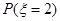 ; (Ⅱ)求随机变量
; (Ⅱ)求随机变量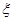 的分布列和它的数学期望.
的分布列和它的数学期望.  户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)
户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)

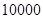 户,在政府进行节水动员前平均每月用水量是
户,在政府进行节水动员前平均每月用水量是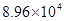 吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;
吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;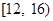 范围内的家庭中选出
范围内的家庭中选出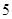 户作为采访对象,其中在
户作为采访对象,其中在 内的抽到
内的抽到 户,求
户,求 ,记政治、历史、地理达到优秀水平的事件分别为
,记政治、历史、地理达到优秀水平的事件分别为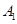 、
、 、
、 ,未达到优秀水平的事件分别为
,未达到优秀水平的事件分别为 、
、 、
、 .
. ,试求事件
,试求事件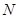 ,使得事件
,使得事件 ,并说明理由.
,并说明理由. .
.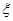 ,求
,求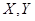 分别表示这4个人中去参加甲、乙项目联欢的人数,记
分别表示这4个人中去参加甲、乙项目联欢的人数,记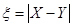 ,求随机变量
,求随机变量 的分布列与数学期望
的分布列与数学期望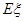 .
.