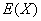题目内容
甲,乙两人进行射击比赛,每人射击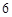 次,他们命中的环数如下表:
次,他们命中的环数如下表:
| 甲 | 5 | 8 | 7 | 9 | 10 | 6 |
| 乙 | 6 | 7 | 4 | 10 | 9 | 9 |
(Ⅱ)把甲6次射击命中的环数看成一个总体,用简单随机抽样方法从中抽取两次命中的环数组成一个样本,求该样本平均数与总体平均数之差的绝对值不超过
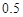 的概率.
的概率.
(1)甲比乙发挥较稳定
(2)
解析试题分析:解 (Ⅰ)甲射击命中的环数的平均数为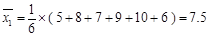 ,
,
其方差为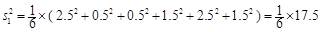 .
.  分
分
乙射击命中的环数的平均数为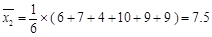 ,
,
其方差为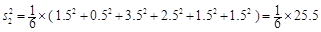 .
. 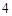 分
分
因此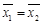 ,
,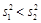 ,故甲,乙两人射击命中的环数的平均数相同,但甲比乙发挥较稳定.
,故甲,乙两人射击命中的环数的平均数相同,但甲比乙发挥较稳定.
(Ⅱ)由(Ⅰ)知,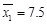 .
.
设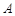 表示事件“样本平均数与总体平均数之差的绝对值不超过
表示事件“样本平均数与总体平均数之差的绝对值不超过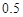 ”.
”.
从总体中抽取两个个体的全部可能的结果 ,
, 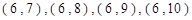

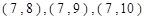 ,
,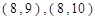 ,
,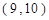 ,共15个结果.其中事件
,共15个结果.其中事件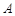 包含的结果有
包含的结果有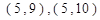

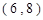 ,
,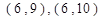

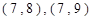 ,共有
,共有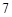 个结果.
个结果. 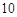 分
分
故所求的概率为 .
.  分
分
考点:古典概型
点评:主要是考查了古典概型的概率的计算,以及方差和均值的运用,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花做垃圾处理.
(Ⅰ)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.
(Ⅱ)花店记录了100 天玫瑰花的日需求量(单位:枝),整理得下表:
| 日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
(ii)若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率.
某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的统计结果如下表:
| 日销售量(吨) | 1 | 1.5 | 2 |
| 天数 | 10 | 25 | 15 |
(2)若以频率为概率,且每天的销售量相互独立.
①求5天中该种商品恰有2天的销售量为1.5吨的概率;
②已知每吨该商品的销售利润为2万元,X表示该种商品两天销售利润的和,求X的分布列和数学期望.
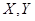 分别表示这4个人中去参加甲、乙项目联欢的人数,记
分别表示这4个人中去参加甲、乙项目联欢的人数,记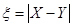 ,求随机变量
,求随机变量 的分布列与数学期望
的分布列与数学期望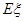 .
.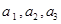 ,女生2名,记为
,女生2名,记为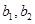 ,现从中任选2名学生去参加校数学竞赛
,现从中任选2名学生去参加校数学竞赛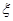 的概率密度函数
的概率密度函数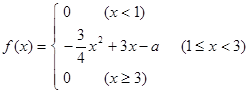 ,
, 的值,并画出
的值,并画出
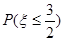 .
. ,求
,求 的分布列及数学期望
的分布列及数学期望