题目内容
5.已知曲线C:y=$\sqrt{4-{x}^{2}}$(0≤x≤2)与函数f(x)=logax及函数g(x)=ax,(其中a>1)的图象分别交于A(x1,y1)、B(x2,y2),则x${\;}_{1}^{2}$+x${\;}_{2}^{2}$的值为4.分析 根据曲线C与f(x)和g(x)的图象分别交于A、B两点,且f(x)与g(x)互为反函数,
得出A与B关于y=x对称,横、纵坐标互换,从而求出x12+x22的值.
解答 解:∵y=$\sqrt{{x}^{2}{+y}^{2}}$,
∴x2+y2=4(0≤x≤2);
又∵曲线C:y=$\sqrt{{x}^{2}{+y}^{2}}$与函数f(x)=logax和函数g(x)=ax(其中a>1)的图象
分别交于A(x1,y1)、B(x2,y2),如图所示;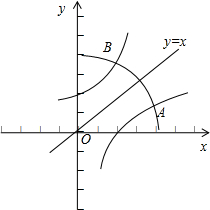
且函数f(x)=logax与函数g(x)=ax互为反函数,
∴A(x1,y1)、B(x2,y2)关于直线y=x对称,
∴x2=y1;
又∵A(x1,y1)在曲线C上,
∴x12+x22=x12+y12=4.
故答案为:4.
点评 本题考查了函数的图象与性质的应用问题,也考查了互为反函数的应用问题,是基础题目.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
17.5人排成一排,甲只能排在第一个或第二两个位置,乙只能排在第二或第三两个位置,不同的排法共有( )
| A. | 12种 | B. | 16种 | C. | 18种 | D. | 24种 |
15.在△ABC中,内角A,B,C所对的边分别是a,b,c,B=60°,a+c=1,则b的取值范围为( )
| A. | [$\frac{1}{2}$,1) | B. | [$\frac{1}{4}$,1) | C. | [$\frac{1}{4}$,$\frac{1}{2}$) | D. | (0,1) |