题目内容
8.设角θ的终边经过点P(4,-3),那么2cosθ-sinθ=( )| A. | 1 | B. | $\frac{11}{5}$ | C. | $-\frac{11}{5}$ | D. | -1 |
分析 由已知三角函数的定义分别求出sinθ和cosθ,代入计算.
解答 解:因为角θ的终边经过点P(4,-3),
所以P到原点的距离为5,由三角函数的定义得到sinθ=$-\frac{3}{5}$,cosθ=$\frac{4}{5}$,
所以2cosθ-sinθ=2×$\frac{4}{5}$+$\frac{3}{5}$=$\frac{11}{5}$;
故选:B.
点评 本题主要课程了三角函数的定义;由角的终边上一点,求三角函数值,根据定义解答.

练习册系列答案
相关题目
18.设数列{an}中,已知a1=1,an=1+$\frac{1}{{{a_{n-1}}}}$(n>1),则a3=( )
| A. | $\frac{8}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
16.执行如图所示的程序框图,输入x=-2,h=0.5,那么输出的各个数的和等于( )
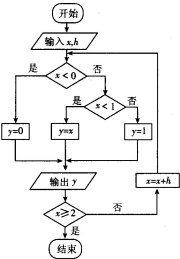

| A. | 3 | B. | 3.5 | C. | 4 | D. | 4.5 |
3.若sinx•cosx<0,则角x的终边位于( )
| A. | 第一、二象限 | B. | 第二、三象限 | C. | 第二、四象限 | D. | 第三、四象限 |
13.函数f(x)=log2(x+1)-$\frac{2}{x}$的其中一个零点所在的区间是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
17.原点与点(2,3)在直线2x+y-3=0的( )
| A. | 同侧 | B. | (2,3)在直线上 | C. | 异侧 | D. | 以上都不对 |