题目内容
20.证明:1,$\sqrt{3}$,2不能为同一等差数列的三项.分析 根据等差数列的定义,利用反证法进行证明.
解答 证明:假设1,$\sqrt{3}$,2为同一等差数列的三项.
可设该等差数列的首项为a,公差为d,
其中1,$\sqrt{3}$,2分别是等差数列的第m、n、k项,
则1=a+(m-1)d,①
$\sqrt{3}$=a+(n-1)d,②
2=a+(k-1)d,③
∴②-①得$\sqrt{3}$-1=(n-m)d,
③-①得1=(k-m)d,
将上面两式相除得:
$\sqrt{3}$-1=$\frac{n-m}{k-m}$
这是不可能的,上式右边是有理数,左边是无理数.
∴假设不成立,
即1,$\sqrt{3}$,2不能为同一等差数列的三项.
点评 本题主要考查反证法的应用,结合等差数列的定义和性质是解决本题的关键.

练习册系列答案
相关题目
8.设角θ的终边经过点P(4,-3),那么2cosθ-sinθ=( )
| A. | 1 | B. | $\frac{11}{5}$ | C. | $-\frac{11}{5}$ | D. | -1 |
12.已知函数f(x)=$\frac{1}{3}$x3-(4m-1)x2+(15m2-2m-7)x+2在R上是增函数,则m的取值范围为( )
| A. | m≤2或m≥4 | B. | -4≤m≤-2 | C. | 2≤m≤4 | D. | 以上皆不对 |
10.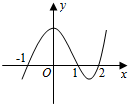 设函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
设函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
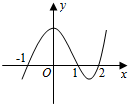 设函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
设函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )| A. | 函数f(x)有极大值f(1)和极小值f(-1) | B. | 函数f(x)有极大值f(1)和极小值f(2) | ||
| C. | 函数f(x)有极大值f(2)和极小值f(1) | D. | 函数f(x)有极大值f(-1)和极小值f(2) |