题目内容
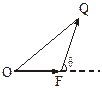
如下图,已知△OFQ的面积为S,且 ·
·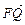 =1,
=1,
(1)若S的范围为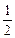 <S<2,求向量
<S<2,求向量 与
与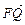 的夹角θ的取值范围;
的夹角θ的取值范围;
(2)设| |=c(c≥2),S=
|=c(c≥2),S= c,若以O为中心,F为焦点的椭圆经过点Q,当|
c,若以O为中心,F为焦点的椭圆经过点Q,当|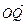 |取得最小值时,求此椭圆的方程.
|取得最小值时,求此椭圆的方程.
 ·
·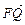 =1,
=1,
(1)若S的范围为
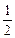 <S<2,求向量
<S<2,求向量 与
与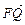 的夹角θ的取值范围;
的夹角θ的取值范围;(2)设|
 |=c(c≥2),S=
|=c(c≥2),S= c,若以O为中心,F为焦点的椭圆经过点Q,当|
c,若以O为中心,F为焦点的椭圆经过点Q,当|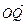 |取得最小值时,求此椭圆的方程.
|取得最小值时,求此椭圆的方程.(1) 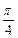 <θ<arctan4.
<θ<arctan4.
 (2) 椭圆方程为
(2) 椭圆方程为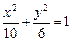 .
.
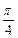 <θ<arctan4.
<θ<arctan4. (2) 椭圆方程为
(2) 椭圆方程为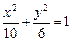 .
.本题考查向量的基本知识、三角知识及最值问题在解析几何中的综合运用.
(1)∵ ·
·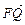 =1,∴|
=1,∴| |·|
|·|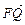 |·cosθ=1.
|·cosθ=1.
又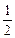 |
| |·|
|·|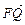 |·sin(180°-θ)=S,
|·sin(180°-θ)=S,
∴tanθ=2S,S=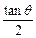 .
.
又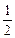 <S<2,∴
<S<2,∴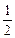 <
<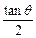 <2,即1<tanθ<4,
<2,即1<tanθ<4,
∴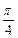 <θ<arctan4.
<θ<arctan4.
(2)以 所在的直线为x轴,以
所在的直线为x轴,以 的过O点的垂线为y轴建立直角坐标系(如下图).
的过O点的垂线为y轴建立直角坐标系(如下图).

∴O(0,0),F(c,0),Q(x0,y0).
设椭圆方程为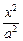 +
+ =1.
=1.
又 ·
·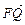 =1,S=
=1,S= c,
c,
∴(c,0)·(x0-c,y0)="1. " ①
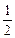 ·c·|y0|=
·c·|y0|= c. ②
c. ②
由①得c(x0-c)=1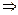 x0=c+
x0=c+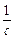 .
.
由②得|y0|=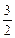 .
.
∴|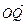 |=
|=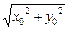 =
=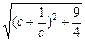 .
.
∵c≥2,
∴当c=2时,|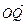 |min=
|min=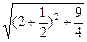 =
=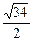 ,
,
此时Q(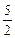 ,±
,±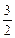 ),F(2,0).
),F(2,0).
代入椭圆方程得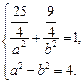
∴a2=10,b2=6.
∴椭圆方程为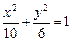 .
.
评析:新知识(向量)在几何中的应用是值得关注的趋势.
(1)∵
 ·
·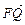 =1,∴|
=1,∴| |·|
|·|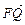 |·cosθ=1.
|·cosθ=1.又
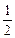 |
| |·|
|·|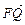 |·sin(180°-θ)=S,
|·sin(180°-θ)=S,∴tanθ=2S,S=
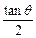 .
.又
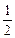 <S<2,∴
<S<2,∴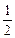 <
<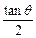 <2,即1<tanθ<4,
<2,即1<tanθ<4,∴
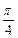 <θ<arctan4.
<θ<arctan4.(2)以
 所在的直线为x轴,以
所在的直线为x轴,以 的过O点的垂线为y轴建立直角坐标系(如下图).
的过O点的垂线为y轴建立直角坐标系(如下图).
∴O(0,0),F(c,0),Q(x0,y0).
设椭圆方程为
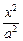 +
+ =1.
=1.又
 ·
·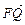 =1,S=
=1,S= c,
c,∴(c,0)·(x0-c,y0)="1. " ①
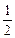 ·c·|y0|=
·c·|y0|= c. ②
c. ②由①得c(x0-c)=1
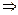 x0=c+
x0=c+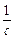 .
.由②得|y0|=
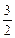 .
.∴|
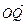 |=
|=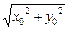 =
=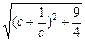 .
.∵c≥2,
∴当c=2时,|
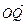 |min=
|min=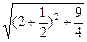 =
=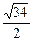 ,
,此时Q(
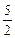 ,±
,±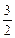 ),F(2,0).
),F(2,0).代入椭圆方程得
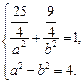
∴a2=10,b2=6.
∴椭圆方程为
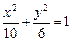 .
.评析:新知识(向量)在几何中的应用是值得关注的趋势.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
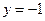 的距离比它到点F
的距离比它到点F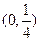 的距离大
的距离大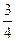 .
.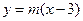 对称,求实数
对称,求实数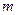 的取值范围.
的取值范围.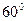 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )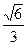
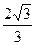
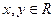 ,
,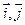 为直角坐标平面内
为直角坐标平面内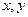 轴正方向上的单位向量,若向量
轴正方向上的单位向量,若向量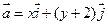 ,
,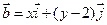 ,且
,且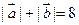 .(1)求点
.(1)求点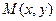 的轨迹
的轨迹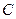 的方程;(2)过点(0,3)作直线
的方程;(2)过点(0,3)作直线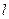 与曲线
与曲线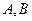 两点,设
两点,设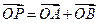 ,是否存在这样的直线
,是否存在这样的直线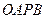 是矩形?若存在,求出直线
是矩形?若存在,求出直线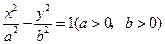 的焦点间的距离,焦点与顶点间的距离,焦点与准线间的距离,准线与准线间的距离,顶点到准线的距离.
的焦点间的距离,焦点与顶点间的距离,焦点与准线间的距离,准线与准线间的距离,顶点到准线的距离.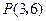 在以两坐标轴为对称轴的椭圆上,你能根据
在以两坐标轴为对称轴的椭圆上,你能根据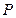 点的坐标最多写出椭圆上几个点的坐标(
点的坐标最多写出椭圆上几个点的坐标(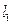 ,
,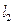 分别过点
分别过点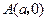 ,
,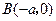 (
(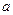 为常数),且分别绕
为常数),且分别绕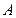 ,
,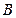 旋转,它们分别交
旋转,它们分别交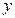 轴于
轴于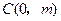 ,
,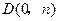 (
(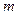 ,
,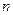 为参数),若
为参数),若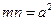 ,求两直线交点
,求两直线交点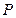 的轨迹方程.
的轨迹方程.