题目内容
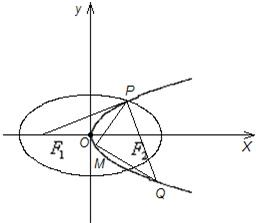
如图,A(-1,0),B(1,0),过曲线C1:y=x2-1(|x|≥1)上一点M的切线l,与曲线C2:y=-
(|x|<1)也相切于点N,记点M的横坐标为t(t>1).
(1)用t表示m的值和点N的坐标;
(2)当实数m取何值时,∠MAB=∠NAB?并求此时MN所在直线的方程.

| m(1-x2) |
(1)用t表示m的值和点N的坐标;
(2)当实数m取何值时,∠MAB=∠NAB?并求此时MN所在直线的方程.

(1)切线l:y-(t2-1)=2t(x-t),即y=2tx-t2-1,
代入y=-
,
化简并整理得(m+4t2)x2-4t(t2+1)x+(t2+1)2-m=0,(*)
由△=16t2(t2+1)2+4(m+4t2)[m-(t2+1)2]=4m[m-(t2-1)2]=0
得m=0或m=(t2-1)2.
若m=0,代入(*)式得xN=
>1,与已知|xN|<1矛盾;
若m=(t2-1)2,代入(*)式得xN=
∈(0,1)满足条件,
且yN=2txN-t2-1=-
,
综上,m=(t2-1)2,点N的坐标为(
,-
).
(2)因为kAM=
=t-1,kAN=
=-(t-1)2,
若∠MAB=∠NAB,则kAM=-kAN,即t=2,此时m=9,
故当实数m=9时,∠MAB=∠NAB.
此时kAM=1,kAN=-1,∠MAB=∠NAB=45°,
易得M(2,3),N(
,-
),
此时MN所在直线的方程为y=4x-5.
代入y=-
| m(1-x2) |
化简并整理得(m+4t2)x2-4t(t2+1)x+(t2+1)2-m=0,(*)
由△=16t2(t2+1)2+4(m+4t2)[m-(t2+1)2]=4m[m-(t2-1)2]=0
得m=0或m=(t2-1)2.
若m=0,代入(*)式得xN=
| t2+1 |
| 2t |
若m=(t2-1)2,代入(*)式得xN=
| 2t |
| t2+1 |
且yN=2txN-t2-1=-
| (t2-1)2 |
| t2+1 |
综上,m=(t2-1)2,点N的坐标为(
| 2t |
| t2+1 |
| (t2-1)2 |
| t2+1 |
(2)因为kAM=
| t2-1 |
| t+1 |
-
| ||
|
若∠MAB=∠NAB,则kAM=-kAN,即t=2,此时m=9,
故当实数m=9时,∠MAB=∠NAB.
此时kAM=1,kAN=-1,∠MAB=∠NAB=45°,
易得M(2,3),N(
| 4 |
| 5 |
| 9 |
| 5 |
此时MN所在直线的方程为y=4x-5.

练习册系列答案
相关题目
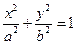 (a>b>0)相交于不同两点A、B,
(a>b>0)相交于不同两点A、B,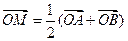 ,且
,且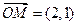 ,以M为焦点,以椭圆的右准线为相应准线的双曲线与直线l相交于N(4,
,以M为焦点,以椭圆的右准线为相应准线的双曲线与直线l相交于N(4,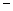 1). (I)求椭圆的离心率
1). (I)求椭圆的离心率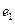 ; (II)设双曲线的离心率为
; (II)设双曲线的离心率为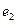 ,记
,记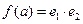 ,求
,求 的解析式,并求其定义域和值域.
的解析式,并求其定义域和值域.