Question

【题目】下列说法中错误的序号是： _________

①已知恒成立，若为真命题，则实数的最大值为2；

②已知三点共线，则的最小值为11；

③已知是椭圆的为两个焦点，点在椭圆上,则使三角形为直角三角形的点个数4 个；

④在圆内，过点有条弦的长度成等差数列，最小弦长为数列的首项，最大弦长为，若公差那么的取值集合为 .

Answer 1

【答案】①③④

【解析】

①根据p与真假相反，判断p的真假，再根据p的真假转化为不等式，求得a的取值范围，即可判断；

②利用向量共线定理，求得a，b的关系式，再利用基本不等式求最值，进而判断；

③先求出椭圆的焦点，再分情况分析三角形为直角三角形的点个数，进而判断；

④由已知条件推导出4+（n-1）d=5，根据d的取值范围，求得4≤n≤6．由此能求出n的值，进而判断.

①已知恒成立，为真命题，则p为假命题，即（x>0）有解，整理得,

∵y=x2-ax+1开口向上，可得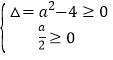 ,解得 ，故①错误；

②已知三点共线，可知 ，

∵=（，1），=（-b-1,2），∴k=，=（-b-1）,整理得2a+b= 1，

∵ ， ，

∴当且仅当时等号成立，即时等号成立.

故 ，当时等号成立，故②正确；

③已知椭圆，即 则 ，

则 ，

由于△PF1F2是直角三角形，根据椭圆的几何性质， 若PF1⊥F1F2，则有两个P使得三角形是直角三角形，若PF2⊥F1F2，则有两个P使得三角形是两个直角三角形，

若PF1⊥PF2，设点P(m，n)，则=（，-n），=（-m,-n），

，结合点P在椭圆上，

解得n= ，故满足题意的点P有4个，

综上所述，使三角形为直角三角形的点有8个 ，故③错误；

④圆x2+y2=5x的圆心为C ，

过点的最短的弦长为

过点的最长的弦长为5

根据等差数列通项公式，4+（n-1）d=5 n*，则，

∵ ，∴ ，解得 ,故的取值集合为，故④错误.

故填：①③④