题目内容
设函数
.
（1）若
的两个极值点为
，且
，求实数
的值；
（2）是否存在实数，使得是
上的单调函数？若存在,求出的值；若不存在，说明理由.
（1）
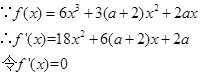
根据韦达定理得：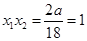
解得：
（2）假设存在实数，使得是上的单调函数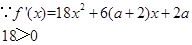
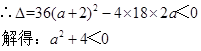
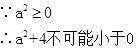
所以不存在实数，使得是上的单调函数.
解析
练习册系列答案
相关题目
题目内容
设函数.
（1）若的两个极值点为，且，求实数的值；
（2）是否存在实数，使得是上的单调函数？若存在,求出的值；若不存在，说明理由.
（1）
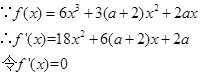
根据韦达定理得：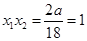
解得：
（2）假设存在实数，使得是上的单调函数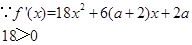
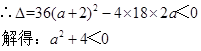
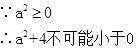
所以不存在实数，使得是上的单调函数.
解析
.
的单调区间；
对
恒成立，求实数
的取值范围.
x3－
x2＋ax．
．
(
) 
的单调递减区间；
，
（1）若函数
在
处与直线
相切；
的值； ②求函数
上的最大值;
时，若不等式
对所有的
都成立，求实数
的取值范围.
,已知
是奇函数。
是奇函数，且图像在点
为自然对数的底数）处的切线斜率为3.
、
的值;
，且
对任意
恒成立，求
的最大值;
时，证明：
（
）若
上是增函数，在（0，1）上是减函数，函数
在R上有三个零点，且1是其中一个零点。
最小值的取值范围。
，
．
[h(x)]
，求F(x)的单调区间与极值；
，解关于x的方程
；
，证明：
．