题目内容
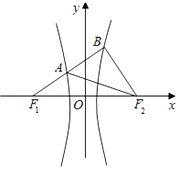
【题目】如图，已知圆G：x2﹣x+y2=0，经过抛物线y2=2px的焦点，过点（m，0）（m＜0）倾斜角为 
的直线l交抛物线于C，D两点． （Ⅰ）求抛物线的方程；
（Ⅱ）若焦点F在以线段CD为直径的圆E的外部，求m的取值范围．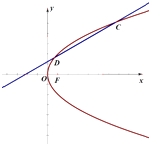
【答案】解：（Ⅰ）∵圆G：x2﹣x+y2=0与x轴交于（0，0），（1，0）， 圆G：x2﹣x+y2=0，经过抛物线y2=2px的焦点，
∴抛物线y2=2px的焦点F（1，0），
∴抛物线的方程为：y2=4x．
（Ⅱ）设C（x1 ， y1），D（x2 ， y2），
∵ 
，则（x1﹣1）（x2﹣1）+y1y2＞0，
设l的方程为： 
，
于是 
即 
由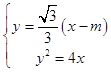 
，得x2﹣（2m+12）x+m2=0，
∴ 
，
于是 
，
故 
，
又△=（2m+12）2﹣4m2＞0，得到m＞﹣3．
∴ 
或m＞2 
．
【解析】（Ⅰ）圆G：x2﹣x+y2=0与x轴交于（0，0），（1，0），从而抛物线y2=2px的焦点F（1，0），由此能求出抛物线的方程．（Ⅱ）设C（x1 ， y1），D（x2 ， y2），则（x1﹣1）（x2﹣1）+y1y2＞0，设l的方程为： 
，则 
，由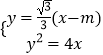 
，得x2﹣（2m+12）x+m2=0，由此利用韦达定理结合已知条件能求出m的取值范围．
练习册系列答案
相关题目
