题目内容
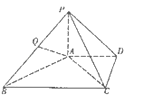
【题目】若二面角α﹣L﹣β的大小为 ![]() ,此二面角的张口内有一点P到α、β的距离分别为1和2,则P点到棱l的距离是( )
,此二面角的张口内有一点P到α、β的距离分别为1和2,则P点到棱l的距离是( )
A.![]()
B.2
C.2 ![]()
D.2 ![]()
【答案】A
【解析】解:设过P,C,D的平面与l交于Q点. 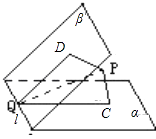
由于PC⊥平面α,l平面M,则PC⊥l,
同理,有PD⊥l,∵PC∩PD=P,
∴l⊥面PCQD于Q.
又 DQ,CQ,PQ平面PCQD
∴DQ⊥l,CQ⊥l.
∴∠DQC是二面角α﹣l﹣β的平面角.
∴∠DQC=60°
且PQ⊥l,所以PQ是P到l的距离.
在平面图形PCQD中,有∠PDQ=∠PCQ=90°
∴P、C、Q、D四点共圆,也为△PDC的外接圆,且PQ是此圆的直径.
在△PCD中,∵PC=1,PD=2,∠CPD=180°﹣60°=120°,
由余弦定理得 CD2=1+4﹣2×1×2×(﹣ ![]() )=7,CD=
)=7,CD= ![]()
在△PDC 中,根据正弦定理 ![]() =2R=PQ,代入数据得出PQ=
=2R=PQ,代入数据得出PQ= ![]() .
.
∴点P到直线l的距离为 ![]()
故选:A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目