Question

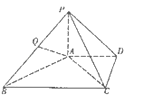
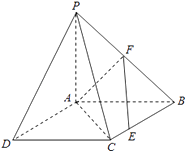
【题目】如图，在几何体P﹣ABCD中，平面ABCD⊥平面PAB，四边形ABCD为矩形，△PAB为正三角形，若AB=2，AD=1，E，F 分别为AC，BP中点．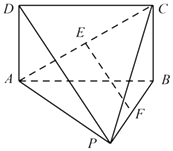
（Ⅰ）求证EF∥平面PCD；
（Ⅱ）求直线DP与平面ABCD所成角的正弦值．

Answer 1

【答案】（Ⅰ）证明：因为E为AC中点，所以DB与AC交于点E． 因为E，F分别为AC，BP中点，所以EF是△BDP的中位线，
所以EF∥DP．
又DP平面PCD，EF平面PCD，
所以EF∥平面PCD．
（Ⅱ）解：取AB中点O，连接PO，DO．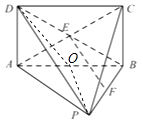

∵△PAB为正三角形，∴PO⊥AB，
又∵平面ABCD⊥平面PAB
∴PO⊥平面ABCD，∴DP在平面ABCD内的射影为DO，∠PDO为DP与平面ABCD所成角，
OP= ，DP= ，在Rt△DOP中，sin∠PDO= ，
∴直线DP与平面ABCD所成角的正弦值为 ．
【解析】（Ⅰ）连结BD，则E为BD的中点，利用中位线定理得出EF∥PD，故而EF∥面PCD；（Ⅱ）取AB中点O，连接PO，DO，得出PO⊥平面ABCD，于是，∠PDO为DP与平面ABCD所成角，求出OP，DP，得直线DP与平面ABCD所成角的正弦值．
【考点精析】关于本题考查的直线与平面平行的判定和空间角的异面直线所成的角，需要了解平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行；已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则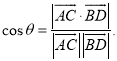才能得出正确答案．