题目内容
【题目】如图,已知海岛A到海岸公路BC的距离AB=50km,B,C间的距离为100km,从A到C必须先坐船到BC上的某一点D,航速为25km/h,再乘汽车到C,车速为50km/h,记∠BDA=θ
(1)试将由A到C所用的时间t表示为θ的函数t(θ);
(2)问θ为多少时,由A到C所用的时间t最少?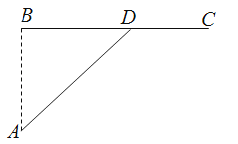
【答案】解:(1)在Rt△ABD中,AB=50km,∴BD=50cotθ,AD=![]() ,∴DC=100﹣BD=100﹣50cotθ.
,∴DC=100﹣BD=100﹣50cotθ.
∴t(θ)=![]() +2﹣cotθ=
+2﹣cotθ=![]() +2(θ∈[arctan
+2(θ∈[arctan![]() ,
,![]() ));
));
(2)t′(θ)=![]() ,
,
∴θ∈[0,![]() )时,t′(θ)<0;θ∈(
)时,t′(θ)<0;θ∈(![]() ,
,![]() ),t′(θ)>0
),t′(θ)>0
∴当![]() 时,由A到C所用的时间t最少.
时,由A到C所用的时间t最少.
【解析】(1)用θ表示出AD与BD,从而可以表示出DC,由路程除以速度得时间,建立起时间关于θ函数即可;
(2)对函数求导,研究出函数的单调性确定出![]() 时,由A到C所用的时间t最少.
时,由A到C所用的时间t最少.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
【题目】假设关于某设备的使用年限x和支出的维修费用y(万元),有如下表的统计资料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知y对x呈线性相关关系,试求:
(1)线性回归方程 ![]() .
.
(2)估计使用年限为10年时,维修费用是多少.
(3)计算总偏差平方和、残差平方和及回归平方和.
(4)求 ![]() 并说明模型的拟合效果.
并说明模型的拟合效果.
