题目内容
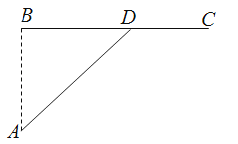
【题目】如图,☉O内切于△ABC的边于点D,E,F,AB=AC,连接AD交☉O于点H,直线HF交BC的延长线于点G. 
(1)求证:圆心O在AD上;
(2)求证:CD=CG;
(3)若AH∶AF=3∶4,CG=10,求HF的长.
【答案】
(1)证明:由题意知AE=AF,CF=CD,BD=BE,而AB=AC,
∴CD=CF=BE=BD.
∴D为BC的中点,
∴AD是∠BAC的平分线,
∴圆心O在AD上.
(2)证明:如图,连接DF.
∵O在AD上,
∴DH为直径,
∴∠DFH=90°.
∵CF=CD,∠CFD=∠FDC,
∴∠G=90°-∠FDC=90°-∠CFD=∠CFG,
∴CG=CF,∴CG=CD.
(3)解:∵∠AFH=90°-∠CFD=90°-∠FDC=∠FDA,又∠FAD为公共角,则△AHF∽△AFD.
∴ ![]()
∴在Rt△HFD中,FH∶FD∶DH=3∶4∶5.
∵△HDF∽△DGF,
∴DF∶GF∶DG=3∶4∶5.
又∵CG=10,∴GD=20.
∴DF=3×20× =12,
∴FH= FD=9.
【解析】本题主要考查了圆的切线的性质及判定定理,解决问题的关键是根据圆的切线的性质及判定定理结合所给图形根据三角形相似性以及边角关系计算即可

【题目】微信已成为人们常用的社交软件,“微信运动”是微信里由腾讯开发的一个类似计步数据库的公众账号.手机用户可以通过关注“微信运动”公众号查看自己每天行走的步数,同时也可以和好友进行运动量的![]() 或点赞.现从小明的微信朋友圈内随机选取了40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下表:
或点赞.现从小明的微信朋友圈内随机选取了40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下表:
步数 性别 | 0 | 2001 | 5001 | 8001 | >10000 |
男 | 1 | 2 | 4 | 7 | 6 |
女 | 0 | 3 | 9 | 6 | 2 |
若某人一天的走路步数超过8000步被系统评定为“积极型”,否则被系统评定为“懈怠型”.
(1)利用样本估计总体的思想,试估计小明的所有微信好友中每日走路步数超过10000步的概率;
(2)根据题意完成下面的![]() 列联表,并据此判断能否有90%的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有90%的把握认为“评定类型”与“性别”有关?
积极型 | 懈怠型 | 总计 | |
男 | |||
女 | |||
总计 |
附: 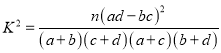
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |