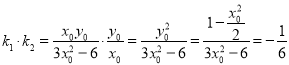题目内容
【题目】将函数![]() 的图像向左平移
的图像向左平移![]() 个单位长度,再将图像上所有点的横坐标伸长到原来的
个单位长度,再将图像上所有点的横坐标伸长到原来的![]() 倍(纵坐标不变),得到
倍(纵坐标不变),得到![]() 的图像.
的图像.
(1)求![]() 的单调递增区间;
的单调递增区间;
(2)若对于任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() .(2)
.(2) ![]() .
.
【解析】
(1)本题首先可通过题意中函数![]() 图像的转化得到
图像的转化得到![]() ,然后通过正弦函数的相关性质即可计算出函数
,然后通过正弦函数的相关性质即可计算出函数![]() 的单调递增区间;
的单调递增区间;
(2)首先通过![]() 计算出函数
计算出函数![]() 的最大值以及最小值,然后将
的最大值以及最小值,然后将![]() 转化为
转化为![]() ,即可列出不等式组
,即可列出不等式组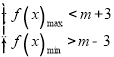 ,通过计算得出结果。
,通过计算得出结果。
(1)函数![]() 的图像向左平移
的图像向左平移![]() 个单位长度可得
个单位长度可得![]() ,
,
然后将![]() 上所有点的横坐标伸长到原来的
上所有点的横坐标伸长到原来的![]() 倍可得
倍可得![]() ,
,
令![]() ,即
,即![]() ,
,
故![]() 的单调递增区间为
的单调递增区间为![]() .
.
(2)因为![]() ,所以
,所以![]() ,
,
所以函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ,此时
,此时![]() ,即
,即![]() ,
,
最小值为![]() ,此时
,此时![]() ,即
,即![]() .
.
对于任意的![]() ,不等式
,不等式![]() 恒成立,
恒成立,
即![]() 恒成立,
恒成立,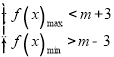 ,
,
所以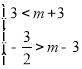 ,
,![]() ,故实数
,故实数![]() 的取值范围为
的取值范围为![]() 。
。

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
【题目】清华大学自主招生考试题中要求考生从A,B,C三道题中任选一题作答,考试结束后,统计数据显示共有600名学生参加测试,选择A,B,C三题答卷数如下表:
题 | A | B | C |
答卷数 | 180 | 300 | 120 |
(Ⅰ)负责招生的教授为了解参加测试的学生答卷情况,现用分层抽样的方法从600份答案中抽出若干份答卷,其中从选择A题作答的答卷中抽出了3份,则应分别从选择B,C题作答的答卷中各抽出多少份?
(Ⅱ)测试后的统计数据显示,A题的答卷得优的有60份,若以频率作为概率,在(Ⅰ)问中被抽出的选择A题作答的答卷中,记其中得优的份数为![]() ,求
,求![]() 的分布列及其数学期望
的分布列及其数学期望![]() .
.