题目内容
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (Ⅰ)求曲线
(Ⅰ)求曲线![]() 的直角坐标方程,并指出其表示何种曲线;(Ⅱ)设直线
的直角坐标方程,并指出其表示何种曲线;(Ⅱ)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若点
两点,若点![]() 的直角坐标为
的直角坐标为![]() ,试求当
,试求当![]() 时,
时,![]() 的值.
的值.
【答案】(1)曲线![]() 的直角坐标方程为
的直角坐标方程为![]() 它表示以
它表示以![]() 为圆心、
为圆心、![]() 为半径的圆.(2)
为半径的圆.(2)![]()
【解析】试题分析:(1)利用参普互化公式将曲线C的方程化为一般方程,进而得到圆心半径;(2)联立直线和园的方程,得到关于t的二次,![]() ,由韦达定理得到结果.
,由韦达定理得到结果.
详解:
(Ⅰ)曲线![]() :
:![]() ,可以化为
,可以化为![]()
![]() ,
,
因此,曲线![]() 的直角坐标方程为
的直角坐标方程为![]()
它表示以![]() 为圆心、
为圆心、![]() 为半径的圆.
为半径的圆.
(Ⅱ)当![]() 时,直线的参数方程为
时,直线的参数方程为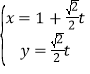 (为参数)
(为参数)
点![]()
![]() 在直线上,且在圆
在直线上,且在圆![]() 内,把
内,把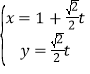
代入![]() 中得
中得![]()
设两个实数根为![]() ,则
,则![]() 两点所对应的参数为
两点所对应的参数为![]() ,
,
则![]() ,
,![]() ,
,![]()

练习册系列答案
相关题目
【题目】已知某海滨浴场海浪的高度![]() (米)是时间
(米)是时间![]() 的(
的(![]() ,单位:小时)函数,记作
,单位:小时)函数,记作![]() ,下表是某日各时的浪高数据:
,下表是某日各时的浪高数据:
| 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
经长期观察,![]() 的曲线,可以近似地看成函数
的曲线,可以近似地看成函数![]() 的图象.
的图象.
(1)根据以上数据,求出函数![]() 近似表达式;
近似表达式;
(2)依据规定,当海浪高度高于![]() 米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午
米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午![]() 时至晚上
时至晚上![]() 时之间,有多少时间可供冲浪者进行运动?
时之间,有多少时间可供冲浪者进行运动?


