题目内容
若有穷数列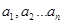 (
(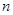 是正整数),满足
是正整数),满足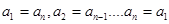 即
即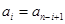 (
(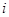 是正整数,且
是正整数,且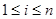 ),就称该数列为“对称数列”。
),就称该数列为“对称数列”。
(1)已知数列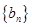 是项数为7的对称数列,且
是项数为7的对称数列,且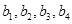 成等差数列,
成等差数列,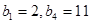 ,试写出
,试写出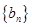 的每一项
的每一项
(2)已知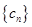 是项数为
是项数为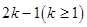 的对称数列,且
的对称数列,且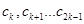 构成首项为50,公差为
构成首项为50,公差为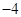 的等差数列,数列
的等差数列,数列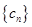 的前
的前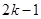 项和为
项和为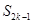 ,则当
,则当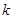 为何值时,
为何值时,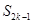 取到最大值?最大值为多少?
取到最大值?最大值为多少?
(3)对于给定的正整数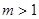 ,试写出所有项数不超过
,试写出所有项数不超过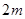 的对称数列,使得
的对称数列,使得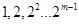 成为数列中的连续项;当
成为数列中的连续项;当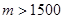 时,试求其中一个数列的前2008项和
时,试求其中一个数列的前2008项和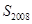
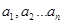 (
(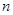 是正整数),满足
是正整数),满足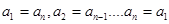 即
即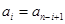 (
(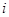 是正整数,且
是正整数,且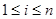 ),就称该数列为“对称数列”。
),就称该数列为“对称数列”。(1)已知数列
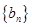 是项数为7的对称数列,且
是项数为7的对称数列,且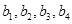 成等差数列,
成等差数列,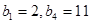 ,试写出
,试写出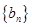 的每一项
的每一项(2)已知
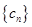 是项数为
是项数为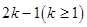 的对称数列,且
的对称数列,且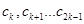 构成首项为50,公差为
构成首项为50,公差为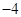 的等差数列,数列
的等差数列,数列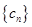 的前
的前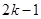 项和为
项和为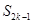 ,则当
,则当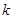 为何值时,
为何值时,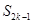 取到最大值?最大值为多少?
取到最大值?最大值为多少?(3)对于给定的正整数
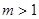 ,试写出所有项数不超过
,试写出所有项数不超过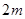 的对称数列,使得
的对称数列,使得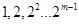 成为数列中的连续项;当
成为数列中的连续项;当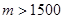 时,试求其中一个数列的前2008项和
时,试求其中一个数列的前2008项和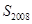
(1)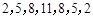 ;(2)626;(3)见解析.
;(2)626;(3)见解析.
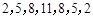 ;(2)626;(3)见解析.
;(2)626;(3)见解析.本试题主要是考查了数列的新的定义,理解概念并能运用所学的求解数列的和的最值问题和数列和的运算。
解:(1)设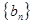 的公差为
的公差为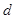 ,则
,则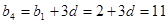 ,解得
,解得 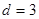 ,
,
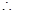 数列
数列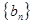 为
为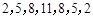 .
.
(2)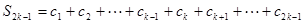
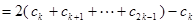 ,
,
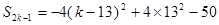 ,
,
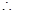 当
当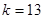 时,
时,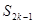 取得最大值.
取得最大值.
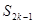 的最大值为626.
的最大值为626.
(3)所有可能的“对称数列”是:
①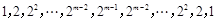 ;
;
②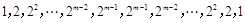 ;
;
③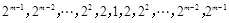 ;
;
④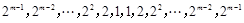 .
.
对于①,当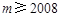 时,
时,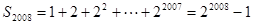 .
.
当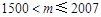 时,
时,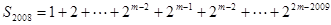
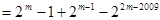
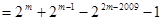 .
.
对于②,当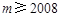 时,
时,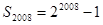 .
.
当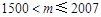 时,
时,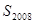
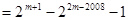 .
.
对于③,当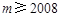 时,
时,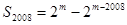 .
.
当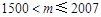 时,
时,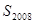
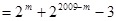 .
.
对于④,当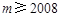 时,
时,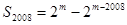 .
.
当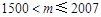 时,
时,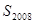
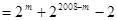 .
.
解:(1)设
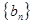 的公差为
的公差为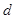 ,则
,则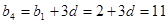 ,解得
,解得 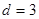 ,
,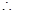 数列
数列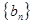 为
为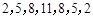 .
. (2)
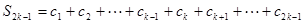
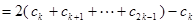 ,
, 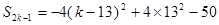 ,
,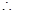 当
当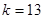 时,
时,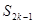 取得最大值.
取得最大值. 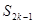 的最大值为626.
的最大值为626. (3)所有可能的“对称数列”是:
①
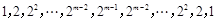 ;
;②
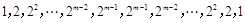 ;
;③
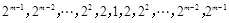 ;
;④
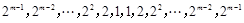 .
. 对于①,当
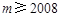 时,
时,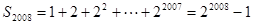 .
. 当
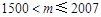 时,
时,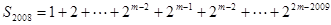
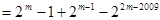
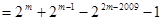 .
. 对于②,当
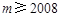 时,
时,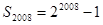 .
. 当
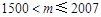 时,
时,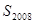
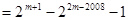 .
.对于③,当
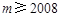 时,
时,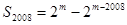 .
. 当
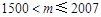 时,
时,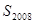
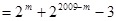 .
.对于④,当
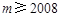 时,
时,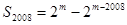 .
. 当
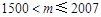 时,
时,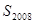
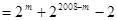 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
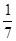 是较少两份面包数之和,问最少的1份面包数为
是较少两份面包数之和,问最少的1份面包数为 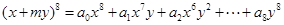 ,若
,若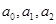 成公差大于0的等差数列,(1)求
成公差大于0的等差数列,(1)求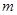 的值;(2)求
的值;(2)求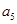 的值;(3)求
的值;(3)求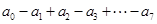 的值.
的值.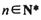 ,总有
,总有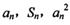 成等差数列.
成等差数列.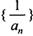 的前n项和为Tn,数列{Tn}的前n项和为Rn,求证:
的前n项和为Tn,数列{Tn}的前n项和为Rn,求证: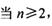
 时,
时,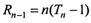 ;
;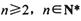 ,试比较
,试比较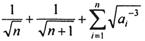 与
与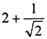 的大小
的大小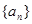 的各项均为正数,
的各项均为正数,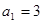 ,前
,前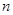 项和为
项和为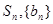 为等比数列,公比
为等比数列,公比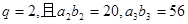 ; (1)求
; (1)求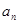 与
与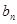 ; (2)求数列
; (2)求数列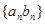 的前
的前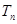 ; (3)记
; (3)记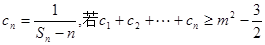 对任意正整数
对任意正整数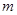 的取值范围。
的取值范围。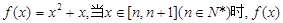 的所有整数值的个数为g(n) .
的所有整数值的个数为g(n) .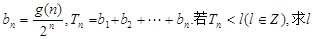 的最小值
的最小值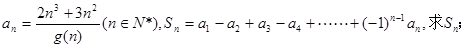
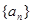 中,
中,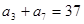 ,则
,则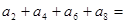 。
。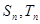 分别是等差数列
分别是等差数列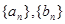 的前
的前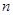 项和,且
项和,且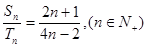 则
则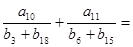
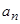 }中,
}中,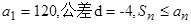 (
(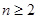 ),则
),则