题目内容
已知数列{an}各项均为正数,Sn为其前n项和,对于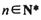 ,总有
,总有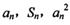 成等差数列.
成等差数列.
(I )求数列{an}的通项an;
(II)设数列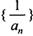 的前n项和为Tn,数列{Tn}的前n项和为Rn,求证:
的前n项和为Tn,数列{Tn}的前n项和为Rn,求证: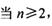
 时,
时,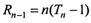 ;
;
(III)对任意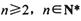 ,试比较
,试比较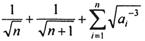 与
与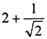 的大小
的大小
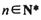 ,总有
,总有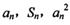 成等差数列.
成等差数列.(I )求数列{an}的通项an;
(II)设数列
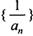 的前n项和为Tn,数列{Tn}的前n项和为Rn,求证:
的前n项和为Tn,数列{Tn}的前n项和为Rn,求证: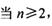
 时,
时,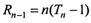 ;
;(III)对任意
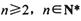 ,试比较
,试比较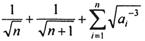 与
与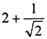 的大小
的大小(I)an=1+(n-1)·1="n" (n∈N*).(2)略 (3)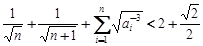
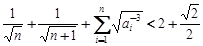
(I )由条件得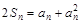 ,递写相减得an+1-an=1,由等差数列求得通项;(II)求出两边表达式证明相等;(III)数学归纳法或不等式证明。
,递写相减得an+1-an=1,由等差数列求得通项;(II)求出两边表达式证明相等;(III)数学归纳法或不等式证明。
解:(I)由题意,得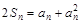 (n∈N*).
(n∈N*).
于是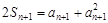 ,
,
两式相减,得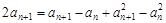 ,
,
即an+1+an=(an+1+an)(an+1-an),
由题,an>0,an+1+an≠0,
得an+1-an=1,即{an}为公差为1的等差数列.
又由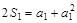 ,得a1=1或a1=0(舍去).
,得a1=1或a1=0(舍去).
∴ an=1+(n-1)·1="n" (n∈N*).……………………………………………5分
(II)证法一:由(I)知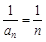 ,于是
,于是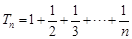 ,
,
于是当n≥2时,
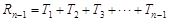 =
=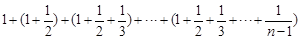
=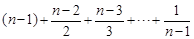
=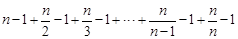
=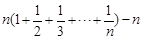 =n(Tn-1). ……………………………10分
=n(Tn-1). ……………………………10分
法二:①当n=2时,R1=T1=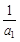 =1,2(T2-1)=2(
=1,2(T2-1)=2(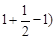 =1,
=1,
∴ n=2时,等式成立.
②假设n=k(k≥2)时,等式成立,即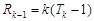 ,
,
当n=k+1时,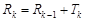
=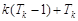 =
= =
=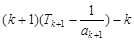
=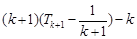 =
=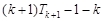 =
=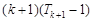 .
.
∴ 当n=k+1时,等式也成立.
综合①②知,原等式对n≥2,n∈N*均成立. …………………………10分
(III)由(I)知,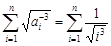 .
.
由分析法易知,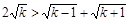 ,
,
当k≥2时,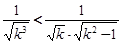
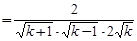

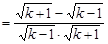
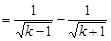 ,∴
,∴ 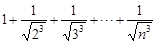
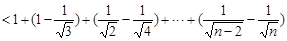
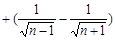
 .即
.即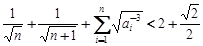 .
.
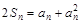 ,递写相减得an+1-an=1,由等差数列求得通项;(II)求出两边表达式证明相等;(III)数学归纳法或不等式证明。
,递写相减得an+1-an=1,由等差数列求得通项;(II)求出两边表达式证明相等;(III)数学归纳法或不等式证明。解:(I)由题意,得
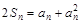 (n∈N*).
(n∈N*).于是
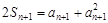 ,
,两式相减,得
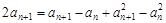 ,
,即an+1+an=(an+1+an)(an+1-an),
由题,an>0,an+1+an≠0,
得an+1-an=1,即{an}为公差为1的等差数列.
又由
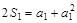 ,得a1=1或a1=0(舍去).
,得a1=1或a1=0(舍去).∴ an=1+(n-1)·1="n" (n∈N*).……………………………………………5分
(II)证法一:由(I)知
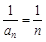 ,于是
,于是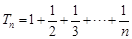 ,
,于是当n≥2时,
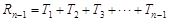 =
=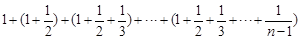
=
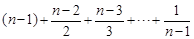
=
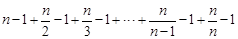
=
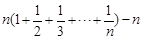 =n(Tn-1). ……………………………10分
=n(Tn-1). ……………………………10分法二:①当n=2时,R1=T1=
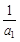 =1,2(T2-1)=2(
=1,2(T2-1)=2(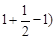 =1,
=1,∴ n=2时,等式成立.
②假设n=k(k≥2)时,等式成立,即
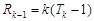 ,
,当n=k+1时,
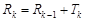
=
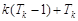 =
= =
=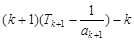
=
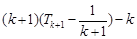 =
=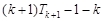 =
=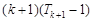 .
.∴ 当n=k+1时,等式也成立.
综合①②知,原等式对n≥2,n∈N*均成立. …………………………10分
(III)由(I)知,
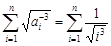 .
.由分析法易知,
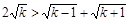 ,
,当k≥2时,
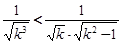
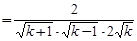

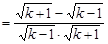
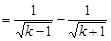 ,∴
,∴ 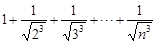
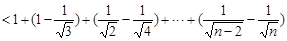
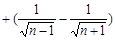
 .即
.即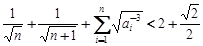 .
.
练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
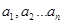 (
(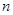 是正整数),满足
是正整数),满足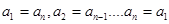 即
即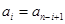 (
(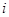 是正整数,且
是正整数,且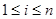 ),就称该数列为“对称数列”。
),就称该数列为“对称数列”。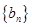 是项数为7的对称数列,且
是项数为7的对称数列,且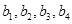 成等差数列,
成等差数列,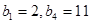 ,试写出
,试写出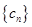 是项数为
是项数为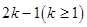 的对称数列,且
的对称数列,且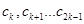 构成首项为50,公差为
构成首项为50,公差为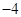 的等差数列,数列
的等差数列,数列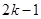 项和为
项和为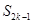 ,则当
,则当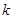 为何值时,
为何值时,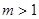 ,试写出所有项数不超过
,试写出所有项数不超过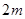 的对称数列,使得
的对称数列,使得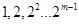 成为数列中的连续项;当
成为数列中的连续项;当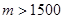 时,试求其中一个数列的前2008项和
时,试求其中一个数列的前2008项和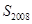
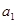 =2,点(
=2,点(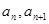 )在函数
)在函数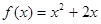 的图像上,其中
的图像上,其中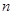 =
=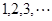 .
.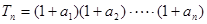 ,求
,求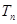 及数列{
及数列{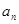 }的通项公式;
}的通项公式;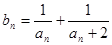 ,求数列{
,求数列{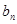 }的前n项和
}的前n项和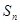 ,并求
,并求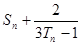 .
.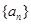 是等差数列,
是等差数列,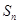 是其前
是其前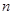 项和,
项和,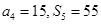 ,则过点
,则过点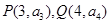 的直线的斜率是( )
的直线的斜率是( )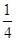
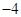
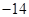
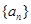 是一个等差数列,且
是一个等差数列,且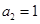 ,
,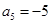 。
。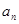 ;
;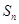 的最大值.
的最大值.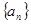 的前
的前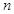 项和为
项和为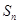 ,若
,若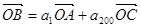 ,且
,且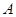 、
、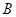 、
、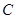 三点共线(该直线不过点
三点共线(该直线不过点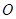 ),则
),则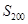 等于( )
等于( )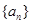 的前n项和为
的前n项和为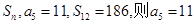 = ( )
= ( )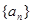 中,
中,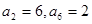 ,则前
,则前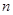 项和
项和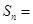 ________.
________.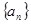 为等差数列,
为等差数列,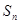 是其前n项的和,且
是其前n项的和,且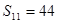 ,则
,则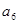 =( )
=( )