题目内容
【题目】已知抛物线E:![]() 的焦点为F,过F的直线l与E交于A,B两点,与x轴交于点
的焦点为F,过F的直线l与E交于A,B两点,与x轴交于点![]() .若A为线段
.若A为线段![]() 的中点,则
的中点,则![]() ( )
( )
A.9B.12C.18D.72
【答案】A
【解析】
解法一:根据![]() 为线段
为线段![]() 的中点,得到
的中点,得到![]() 坐标,从而得到直线
坐标,从而得到直线![]() ,与抛物线联立得到
,与抛物线联立得到![]() ,从而得到
,从而得到![]() ,利用抛物线焦点弦公式,得到
,利用抛物线焦点弦公式,得到![]() 的长;解法二:延长
的长;解法二:延长![]() 交准线
交准线![]() 于
于![]() ,过点
,过点![]() 作
作![]() 垂直准线交准线于
垂直准线交准线于![]() ,过点
,过点![]() 作
作![]() 垂直准线交准线于
垂直准线交准线于![]() ,准线与
,准线与![]() 轴交于点
轴交于点![]() ,由
,由![]() ,得到
,得到![]() ,得到
,得到![]() ,再根据
,再根据![]() ,得到
,得到![]() 的长.
的长.
依题意得![]() ,焦点
,焦点![]() ,
,
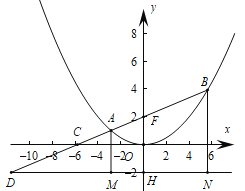
如图,因为![]() 为线段
为线段![]() 的中点,
的中点,
所以![]() ,代入抛物线方程得到
,代入抛物线方程得到![]() ,舍去正值,
,舍去正值,
所以![]() ,
,
解法一: ,
,
所以直线![]() 的方程为
的方程为![]() ,
,
将其代入![]() ,得
,得![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
, ,
,
所以![]() ,
,
故选:A.
解法二:(几何法)延长![]() 交准线
交准线![]() 于
于![]() ,过点
,过点![]() 作
作![]() 垂直准线交准线于
垂直准线交准线于![]() ,
,
过点![]() 作
作![]() 垂直准线交准线于
垂直准线交准线于![]() ,准线与
,准线与![]() 轴交于点
轴交于点![]() ,
,
![]() 中原点
中原点![]() 是线段
是线段![]() 的中点,
的中点,
所以点![]() 是线段
是线段![]() 的中点.易得
的中点.易得![]() ,
,
![]() ,
,![]() ,
,
设![]() ,
,
因为![]() ,
,
所以![]() ,
,
即![]() ,
,
解得![]() ,
,
因此![]() ,
,
故选:A.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】在“创文创卫”活动中,某机构为了解一小区成年居民“吸烟与性别”是否有关.从该小区中随机抽取200位成年居民,得到下边列联表:已知在全部200人中随机抽取1人,抽到不吸烟的概率为0.75.
吸烟 | 不吸烟 | 合计 | |
男 | 40 | ||
女 | 90 | ||
合计 | 200 |
(1)补充上面的列联表,并判断:能否有99.9%的把握认为“吸烟与性别”有关;
(2)用分层抽样的方法从吸烟居民中选5人出来,然后再从中抽2人出来,给小区居民谈谈吸烟的危害性,求恰好抽到“一男一女”的概率.
参考公式: 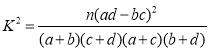 .
.
参考数据:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |