题目内容
6．若关于x的方程x2+（a-1）x+1=0有两相异实根，且两根均在区间[0，2]上，求实数a的取值范围．分析 设f（x）=x2+（a-1）x+1，由题意可得判别式大于0，且f（0）＞0，f（2）不小于0，且对称轴介于[0，2]，解不等式，即可得到所求范围．
解答 解：设f（x）=x2+（a-1）x+1，
由方程有两相异实根，且两根均在区间[0，2]上，
即有$\left\{\begin{array}{l}{△=（a-1）^{2}-4＞0}\\{0＜-\frac{a-1}{2}≤2}\\{f（0）=1＞0}\\{f（2）=4+2（a-1）+1≥0}\end{array}\right.$，
即为$\left\{\begin{array}{l}{a＞3或a＜-1}\\{-3≤a＜1}\\{a≥-\frac{3}{2}}\end{array}\right.$，
解得-$\frac{3}{2}$≤a＜-1．
则实数a的取值范围是[-$\frac{3}{2}$，-1）．
点评 本题考查二次函数和二次方程的关系，考查二次方程实根分布的解法，属于中档题．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
，函数
的定义域为
，则
为（ ）
B．
C．
D．
17．以平面直角坐标系的原点为极点，x轴的正半轴为极轴，建立极坐标系，两种坐标系中取相同的长度单位，已知圆C的参数方程是$\left\{\begin{array}{l}{x=cosθ-1}\\{y=sinθ-1}\end{array}\right.$（θ为参数），直线l的极坐标方程是ρcosθ+ρsinθ=2，则圆C上的点到直线l的最短距离为（ ）
| A． | 2$\sqrt{2}$-1 | B． | 2$\sqrt{2}$+1 | C． | $\sqrt{2}$ | D． | 2$\sqrt{2}$ |
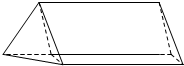如图所示，放置在水平上的组合体由直三棱柱ABC-A1B1C1与正三棱柱B-ABCD组成（D在B1B的延长线上），它的正视图，俯视图，侧视图的面积分别为$2\sqrt{2}+1，2\sqrt{2}+1，1$．